Question

An isosceles triangle has a base of 20cm and legs measuring 36cm. How long are the legs of a similar triangle with a base measuring 50cm?

Answer 1

Hint: In this problem, we are given that an isosceles triangle has a base of 20cm and legs measuring 36cm, we have to find how long are the legs of a similar triangle with base measuring 50cm. We can see that we are given a similar triangle, where corresponding sides of the similar triangles are proportional. We can equate the breadth and length and substitute the given values to find the length of the triangle.

Complete step by step solution:

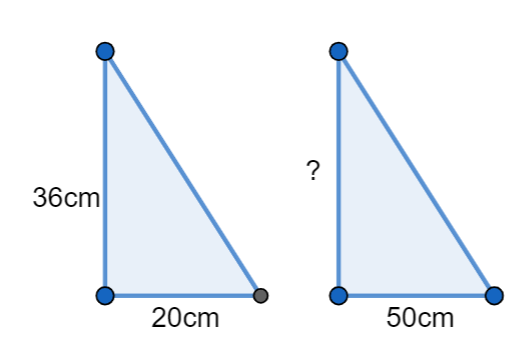
We are given an isosceles triangle has a base of 20cm and legs measuring 36cm.
We have to find how long are the legs of a similar triangle with a base measuring 50cm.
We can see that we are given similar triangles, where corresponding sides of the similar triangles are proportional.
We can write it as,
\[\Rightarrow \dfrac{{{b}_{1}}}{{{l}_{1}}}=\dfrac{{{b}_{2}}}{{{l}_{2}}}\]……. (1)
Given that, \[{{b}_{1}}=20cm,{{b}_{2}}=50cm,{{l}_{1}}=36cm\]
We can now substitute the above values in (1), we get
\[\begin{align}
  & \Rightarrow \dfrac{20}{36}=\dfrac{50}{{{l}_{2}}} \\
 & \Rightarrow {{l}_{2}}=\dfrac{36}{20}\times 50 \\
\end{align}\]
We can now simplify the above step, we get
\[\Rightarrow {{l}_{2}}=90cm\]
Therefore, the required length of the triangle is 90cm.

Note: We should always remember that, for similar triangles the corresponding sides are proportional. We should always remember that we can use the Pythagoras theorem formula, if the given triangle is a right-angled triangle as we are given an isosceles triangle, which is a right-angled one.