Question

An iron pipe 20 cm long has exterior diameter equal to 25 cm. If the thickness of the pipe is 1 cm, find the whole surface area of the pipe.

Answer 1

Hint: We will find the total surface area of the pipe as (surface area of the external pipe + surface area of the internal pipe + 2 $\times $ area of the corner rings of the pipe). The surface area of the pipe is given as $2\pi rl$, which $r$ is the radius of the pipe and $l$ is the length of the pipe. Also, the area of the ring will be $2\left( \pi {{R}^{2}}-\pi {{r}^{2}} \right)$.

Complete step-by-step solution -
It is given in the question that, an iron has length 20 cm and it has exterior diameter of 25 cm and it’s thickness is 1 cm, then we have to find the total surface area of the pipe. Total surface area of the pipe as (surface area of the external pipe + surface area of the internal pipe + 2 $\times $ area of the corner rings of the pipe). We know that the surface area of the pipe is given as $2\pi rl$, where $r$ is the radius of the pipe and $l$ is the length of the pipe. Also, the area of the ring will be $2\left( \pi {{R}^{2}}-\pi {{r}^{2}} \right)$, where $R$ is radius of the external ring and $r$ is the radius of the internal ring.

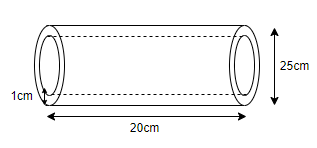
The external radius $\left( R \right)=\dfrac{diameter}{2}\Rightarrow \dfrac{25}{2}cm$
So, the external surface area of the pipe = $2\pi Rl\Rightarrow 2\times \dfrac{22}{7}\times \dfrac{25}{2}\times 20\Rightarrow \dfrac{22000}{14}\Rightarrow 1571.42c{{m}^{2}}$
Internal radius $\left( r \right)=\dfrac{diameter}{2}-1\Rightarrow \dfrac{25}{2}-1\Rightarrow \dfrac{23}{2}cm$
So, the internal surface area of the pipe = $2\pi rl\Rightarrow 2\times \dfrac{22}{7}\times \dfrac{23}{2}\times 20\Rightarrow \dfrac{20240}{14}\Rightarrow 1445.71c{{m}^{2}}$
Now, the surface area of 2 rings at the corner of the pipe = $2\left( \pi {{R}^{2}}-\pi {{r}^{2}} \right)$
$\begin{align}
  & =2\times \left( \dfrac{22}{7}\times \dfrac{25}{2}\times \dfrac{25}{2}-\dfrac{22}{7}\times \dfrac{23}{2}\times \dfrac{23}{2} \right) \\
 & =2\times \left( \dfrac{13750}{28}-\dfrac{11638}{28} \right) \\
 & =2\times \left( 491.07-415.64 \right) \\
 & =2\times 75.43 \\
 & =150.86c{{m}^{2}} \\
\end{align}$
Total surface area of the pipe is = (total surface area of the external pipe + total surface area of the internal pipe + 2 $\times $ surface area of the corner ring).
$\begin{align}
  & =\left( 1571.42+1445.71+150.86 \right)c{{m}^{2}} \\
 & =3167.99c{{m}^{2}}\approx 3168c{{m}^{2}} \\
\end{align}$
Therefore, we get the total surface area of the pipe as $3168c{{m}^{2}}$.

Note: Generally, the students forget to multiply the surface area of the ring by 2, but as we have two rings, we have to multiply the surface area of the ring by 2. The students may also get confused with the formulas. So, it is better for the students to learn all the basic formulas, in order to solve questions like this.