Question

An inverted cone has a depth of 40 cm and a base of radius 5 cm. Water is poured into it at a rate of 1.5 cubic centimetres per minute. Find the rate at which the level of water in the cone is rising when the depth is 4 cm.

Answer 1

Hint: In this question draw a diagram to get a visual representation of the problem. After that use the basic proportionality theorem to find the relation between the two triangles formed. Use this relation in the formula of volume and differentiate the obtained equation so that you obtain the value of $\dfrac{{dh}}{{dt}}$ which will be the required answer.

Complete step-by-step answer:

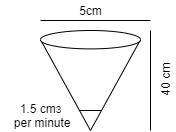We know that volume of a cone = $\dfrac{1}{3}\pi {r^2}h$ equation (1)
Let the height of the water level be h and radius be r. So according to B.P.T., $\dfrac{5}{{40}} = \dfrac{r}{h}$ …. equation (2) One solving equation (1) we get, r =$\dfrac{h}{8}$ … equation (3)
Putting values of equation (3) in equation (1) we get, V = $\dfrac{1}{3}\pi {(\dfrac{h}{8})^2}h$ … equation (4) So, differentiating both sides on equation (4) we get $\dfrac{{dv}}{{dt}} = \dfrac{d}{{dt}}(\dfrac{{\pi {h^3}}}{{192}})$ According to question , we are given the rate at which the level of water in the cone is rising $\dfrac{{dv}}{{dt}} = 1.5$ So, 1.5 =$\dfrac{d}{{dt}}(\dfrac{{\pi {h^3}}}{{192}})$
$\dfrac{{\pi {h^2}}}{{64}}\dfrac{{dh}}{{dt}} = 1.5$ $\dfrac{{dh}}{{dt}} = \dfrac{{96}}{{\pi {h^2}}}$
Now, when h = 4
$\dfrac{{dh}}{{dt}} = \dfrac{6}{\pi }cm/s$
Note: In the above question we used a term differentiation that has many applications in real life. One of its very important applications of derivatives is found in its use in the calculation of the rate of change of quantity in relation to other quantities.