Question

An intense stream of water of cross section area $A$ strikes a wall at an angle $\theta $ with the normal to the wall and returns back elastically. if the density of water is $\rho $ and its velocity is $v$, then the force exerted on the wall will be:
A. $2A{{v}^{2}}$
B. $2A{{v}^{2}}\rho $
C. $2A{{v}^{2}}\rho \cos \theta $
D. $2A{{v}^{2}}\rho \sin \theta $

Answer 1

Hint: By seeing the word elastically along with velocity, and the question asked is Force, we must firstly think of change in change in momentum. Here, we will find the change in momentum of the water stream. The change in momentum of the water stream, directed perpendicular to the wall, is the force exerted by the water stream on the wall.

Formula Used:
$F=\dfrac{\Delta P}{\Delta t}$

Complete answer:
Here, we need to find the force exerted by the water stream on the wall. The word elasticity along with velocity has already hinted us that we shall use the change in momentum formula.
Let’s visualize the question in the form of a diagram.

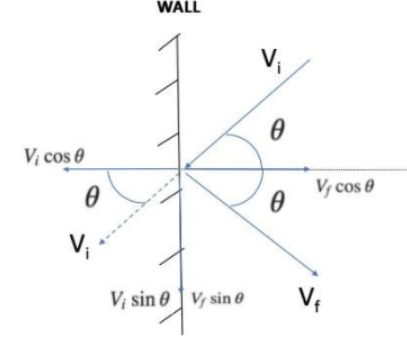
We know that the force applied on the body is nothing but the change in the momentum of that body.
$F=\dfrac{\Delta P}{\Delta t}$ ----(i)
Here, force on the water stream is nothing but the change in its momentum. And the water stream exerts the same force on the wall. Thus, the force exerted on the wall is nothing but the change in the momentum of water.
Here, we need to find the force per second. Hence, above formula (i) can be modified as:
$F=\Delta P$ ----(ii)
We know, the mass of the water stream per second is given by:
$\text{Mass = volume}\times \text{density}$
$m\text{ }=\text{ }V\times \rho $
Here, volume of water stream per second = $\text{Area}\times \text{velocity = }A\times v$
Thus, $mass=Area\times velocity\times density$
$\Rightarrow m=A\times v\times \rho $ ----(iii)
Now,
$F=\Delta P={{P}_{f}}-{{P}_{i}}$
So, $F=m{{v}_{f}}-m{{v}_{i}}$
Here, the force applied on the wall is only due to the component perpendicular to the wall because it is this component that will exert force on the wall. This is the cos component of the momentum. The sin component is along the wall and hence doesn’t exert any force on the wall. Hence it can be neglected.
Thus, force on the wall is given as:
$F=m{{v}_{f}}\cos \theta -(-m{{v}_{i}}\cos \theta )$
Also, the collision here is of elastic nature. Hence the initial and the final velocity of the water stream will remain the same.
Hence,
${{v}_{f}}={{v}_{i}}=v(let)$
Then, $F=2mv\cos \theta $
Using, equation (iii), we replace $m$:
Thus, $F=2A{{v}^{2}}\rho \cos \theta $

Hence, the correct option is (c).

Note:
Here, we neglected the $\sin $ component as this component is tangent to the wall and hence does not exert any force on the wall. This component only grazes past the wall and doesn't exert any pressure or force on it. In elastic collisions the initial and final velocity of the body remains the same after the collision.