Question

An insulating thin rod of length $ l $ as a $ x $ linear charge density $ p\left( x \right) = {p_o}\dfrac{x}{l} $ on it. The rod is rotated about an axis passing through the origin $ \left( {x = 0} \right) $ and perpendicular to the rod. If the rod makes $ n $ rotations per second, then time averaged magnetic moment of the rod is
(A) $ \dfrac{\pi }{4}n\rho {l^3} $
(B) $ n\rho {l^3} $
(C) $ \pi n\rho {l^3} $
(D) $ \dfrac{\pi }{3}n\rho {l^3} $

Answer 1

Hint : To find the magnetic moment of the whole rod, we need to first take an elementary area on the rod and find the magnetic moment due to that area. The magnetic moment of the whole rod can be then found by integrating that value over the whole length of the rod.

Formula Used: In this solution we will be using the following formula,
 $ \Rightarrow dM = \left( {\dfrac{{dq}}{T}} \right)A $
where $ M $ is the magnetic moment,
 $ q $ is the charge enclosed,
 $ T $ is the time period and
 $ A $ is the area enclosed.

Complete step by step answer
According to the question we have a thin insulating rod which is making $ n $ rotations per second about the origin $ \left( {x = 0} \right) $ . So the time period of rotation is the number of rotations performed per second. So we can get the time period of the rotation of the rod as one divided by $ n $ .
So, $ T = \dfrac{1}{n} $
Now let us consider an elementary portion of the rod as $ dx $ . This portion is at a distance $ x $ from the origin.

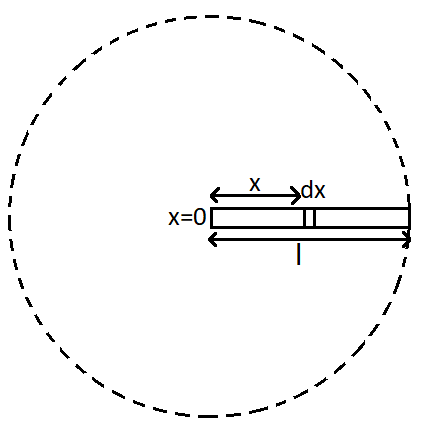
We can draw the figure as above depicting the elementary part.
Now the total area covered by the rod will be the area of the dotted circle from the figure. So the area covered by the rod till the length $ x $ will be,
 $ \Rightarrow A = \pi {x^2} $
Now the linear charge density of the rod is given as $ p\left( x \right) = {p_o}\dfrac{x}{l} $ . So the charge contained in the elementary portion of the rod is
 $ \Rightarrow dq = p\left( x \right)dx $
So substituting we get,
 $ \Rightarrow dq = {p_o}\dfrac{x}{l}dx $
Now the magnetic moment for the part $ dx $ is given by the formula,
 $ \Rightarrow dM = \left( {\dfrac{{dq}}{T}} \right)A $
So substituting all the values we have,
 $ \Rightarrow dM = \dfrac{{{p_o}\dfrac{x}{l}dx}}{{\dfrac{1}{n}}} \times \pi {x^2} $
On simplifying we get,
 $ \Rightarrow dM = \dfrac{{n\pi {p_o}}}{l}{x^3}dx $
So the whole magnetic moment of the rod will be given by integrating $ dM $ over the limits 0 to $ l $ . So we have,
 $ \Rightarrow M = \int_0^l {\dfrac{{n\pi {p_o}}}{l}{x^3}dx} $
As $ \dfrac{{n\pi {p_o}}}{l} $ are constants, so they come out of the integration and then integrating the variable we get,
 $ \Rightarrow M = \dfrac{{n\pi {p_o}}}{l}\left. {\left( {\dfrac{{{x^4}}}{4}} \right)} \right|_0^l $
So putting the limits we get,
 $ \Rightarrow M = \dfrac{{n\pi {p_o}}}{l} \times \dfrac{{{l^4}}}{4} $
On cancelling common terms and arranging we have,
 $ \Rightarrow M = \dfrac{\pi }{4}n{p_o}{l^3} $
Hence the average magnetic moment of the rod is $ \dfrac{\pi }{4}n{p_o}{l^3} $ .
So the correct answer is option (A).

Note
The magnetic moment is the strength and orientation of a magnet or any other object that produces a magnetic field. Since the magnetic moment is given by the product of current and the area so the SI unit of magnetic moment is $ A - {m^2} $ .