Question

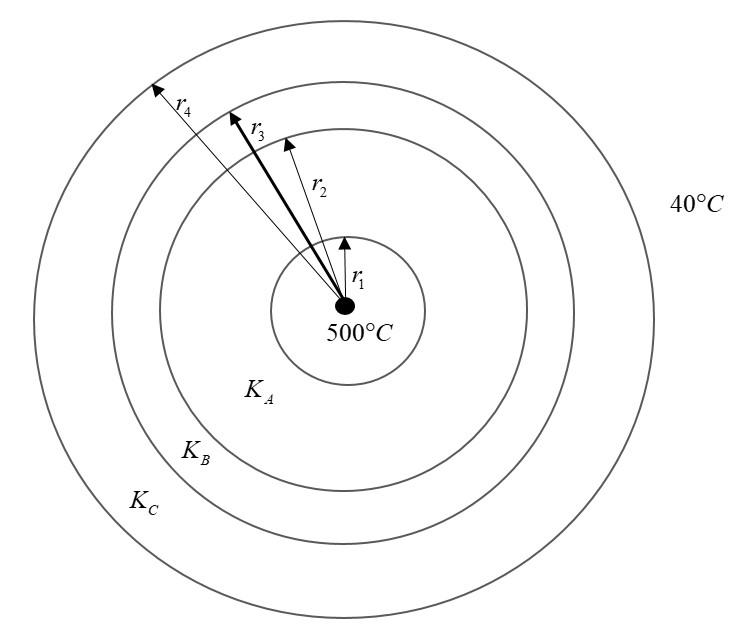
An insulated cylindrical tube of an air-conditioner’s condenser contains a hot fluid. Temperature of fluid is $500^{\circ}C$ and outside temperature is $40^\circ C$. Hot fluid tube is very thin and is covered with 3 layers of different insulating materials. Cross section of the tube is as shown in figure. Given $r_1 = 1 \ cm;\ r_2 = 2\ cm; r_3 = 8\ cm; r_4 = 64\ cm$
Also $K_A = 1Wm^{-1}C^{-1}; K_B = 2Wm^{-1}C^{-1}; K_C = 3Wm^{-1}C^{-1}$:
Heat loss per unit length (in watts) of tube will be:

$\text{A.} \quad \dfrac{460}{ln\ (2)}$
$\text{B.} \quad \dfrac{460}{\pi ln\ (2)}$
$\text{C.} \quad \dfrac{460\pi}{ln\ (2)}$
$\text{D.} \quad \dfrac{2\pi\times 460}{3ln\ (2)}$

Answer 1

Hint: Since the temperature difference is constant with time, so all the heat flowing from hotter fluid to environment will also flow through all the cylindrical shells. This suggests that all the shells are connected in series. Thus the net thermal resistance of the system is the sum of individual thermal resistances.
Formula used:
$R_{net} = R_1 +R_2 +R_3+ . . . ; R_{cylindrical} = \dfrac{1}{2\pi Kl}ln(\dfrac{r_2}{r_1}); \ where \ R=\dfrac{l}{KA}$

Complete answer:
Now, let us find the equivalent resistance of the system consisting of three such cylindrical cavities:
$R_{net} = R_1+R_2+R_3$
${{R}_{net}}=\dfrac{1}{2\pi {{K}_{A}}l}ln\left( \dfrac{{{r}_{2}}}{{{r}_{1}}} \right)+\dfrac{1}{2\pi {{K}_{B}}l}ln\left( \dfrac{{{r}_{3}}}{{{r}_{2}}} \right)+\dfrac{1}{2\pi {{K}_{C}}l}ln\left( \dfrac{{{r}_{4}}}{{{r}_{3}}} \right)$
${{R}_{net}}=\dfrac{1}{2\pi l}\left[ \dfrac{ln\left( \dfrac{{{r}_{2}}}{{{r}_{1}}} \right)}{{{K}_{A}}}+\dfrac{ln\left( \dfrac{{{r}_{3}}}{{{r}_{2}}} \right)}{{{K}_{B}}}+\dfrac{ln\left( \dfrac{{{r}_{4}}}{{{r}_{3}}} \right)}{{{K}_{C}}} \right]$

On putting values:
$r_1 = 1 \ cm; \quad \ r_2 = 2\ cm; \quad r_3 = 8\ cm; \quad r_4 = 64\ cm$
$K_A = 1Wm^{-1}C^{-1};\quad K_B = 2Wm^{-1}C^{-1};\quad K_C = 3Wm^{-1}C^{-1}$
${{R}_{net}}=\dfrac{1}{2\pi l}\left[ \dfrac{ln\left( \dfrac{{2}}{{1}} \right)}{{1}}+\dfrac{ln\left( \dfrac{{8}}{{2}} \right)}{{2}}+\dfrac{ln\left( \dfrac{{64}}{{8}} \right)}{{3}} \right]$
$R_{net} = \dfrac{1}{2\pi l} \left( ln(2) + \dfrac12 ln(2)^2 + \dfrac 13 ln(2)^3 \right)$
$R_{net} = \dfrac{1}{2\pi l} \left( ln(2) + \dfrac22 ln(2) + \dfrac 33 ln(2) \right)$ [as $log(a^b)=b\times log(a)$]
$R_{net} = \dfrac{1}{2\pi l} \left( ln(2) + \dfrac22 ln(2) + \dfrac 33 ln(2) \right)$
$R_{net} = \dfrac{1}{2\pi l} \left( ln(2) + ln(2) + ln(2) \right) = \dfrac{3ln(2)}{2\pi l}$
Now, using the law:
$\dfrac{dQ}{dt} = \dfrac{KA\Delta T}{l}$
Or $\dfrac{dQ}{dt} = \dfrac{\Delta T}{R}$[$as \ R = \dfrac{l}{KA}$]
Hence $\dfrac{dQ}{dt} = \dfrac{500-40}{\dfrac{3 \ ln(2)}{2\pi l}} = \dfrac{2\pi l \times 460}{3\ ln(2)}$
Now, rate of heat flow per unit length = $\dfrac{1}{l}\dfrac{dQ}{dt} = \dfrac{2\pi 460}{3\ ln(2)}$

So, the correct answer is “Option D”.

Additional Information:
In heat flow, we can use the analogy between heat flow and current flow. In heat flow, we have the relation $\dfrac{dQ}{dt} = \dfrac{KA\Delta T}{l}$ and in electricity, we have relation $V=IR$, known as ohm’s law. We can replace $\dfrac{l}{KA} \ with \ R; \ V \ with\ \Delta T \ and \ I\ with\ \dfrac{dQ}{dt}$. We can then also apply the concept of net equivalent of combination of resistances in series and parallel.

Note:
In the question, the heat flowing in the system is the same for all the three cylinders. Hence we can easily say that the cylinders are in series. But suppose the cylinders were connected in such a way that the temperature difference between the three cylinders is the same, in that case the cylinders are said to be connected in parallel and then the net resistance will be the reciprocal of the sum of individual resistances.