Question

An insect crawls up 5cm every second on a 60cm vertical rod and then falls down 2cm over the next second. How many seconds will it take to climb the rod?
A. 20 seconds
B. 39 seconds
C. 60 seconds
D. 30 seconds

Answer 1

Hint: Distance Speed Time Formula
Speed is a measure of how quickly an object moves from one place to another. It is equal to the distance travelled divided by the time. It is possible to find any of these three values using the other two. This picture is helpful:
          

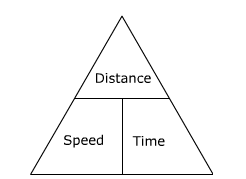
The positions of the words in the triangle show where they need to go in the equations. To find the speed, distance is over time in the triangle, so speed is distance divided by time. To find distance, speed is beside time, so distance is speed multiplied by time.
\[
  Speed = \dfrac{{Distance}}{{time}} \\
  time = \dfrac{{Distance}}{{Speed}} \\
  Distance = speed{\times} time \\
 \]

Complete step-by-step answer:
The insect crawls 5 cm in a second, then falls down 2 cm every next second.
So, it climb \[\left( {5 - 2} \right) = {\text{ }}3{\text{ }}cm\;per\;2\;sec\]
The rod is of 60 cm
Every two seconds, the insect climbs up 3 cm

We will use distance, time and speed formula.
The distance travelled by insect to climb the rod: (as the speed mentioned is for 2 sec so we will half the time in every statement)

In 30 seconds, the insect climbs up \[15{\rm X}3{\text{ }} = {\text{ }}45{\text{ }}cm\]

In 36 seconds, the insect climbs up \[18{\rm X}3{\text{ }} = {\text{ 54 }}cm\]

In 38 seconds, the insect climbs up \[19{\rm X}3{\text{ }} = {\text{ 57 }}cm\]

Now, in the next second it will climb up 5 cm.

Total distance climbed up by the insect in 39 seconds = 57 + 5 = 62 cm

So a total of 39 seconds would be required by the insect to climb the rod.

So, the correct answer is “Option B”.

Note: Speed, distance, and time problems ask to solve for one of the three variables given certain information. In these problems, objects are moving at either constant speeds or average speeds.
Most problems will give values for two variables and ask for the third.