Question

An infinite cylinder of radius $ 'R' $ carrying charge density $ \rho = ar + b{r^2} $ where $ 'r' $ distance of point from the axis and $ a $ , $ b $ are non-zero constant. Find the ratio of $ \dfrac{a}{b} $ if the field out of the cylinder is zero.
 $ \left( A \right)\dfrac{R}{4} \\
  \left( B \right) - \dfrac{R}{4} \\
  \left( C \right) - \dfrac{{3R}}{4} \\
  \left( D \right)\dfrac{{3R}}{4} \\ $

Answer 1

Hint : In order to solve this question, we are going to first draw a figure for the situation as given in the question, then by using the formulae for the flux and the net current and further simplifying the equations and solving for the ratio $ \dfrac{a}{b} $ , we can find the right answer.
The flux of the field is given by
 $ \phi = \dfrac{{{q_{net}}}}{{{\varepsilon _0}}} $
Where flux is the surface integral of an electric field.

Complete Step By Step Answer:
It is given that the radius of the infinite cylinder is $ 'R' $
The charge density is given by $ \rho = ar + b{r^2} $
The distance of point from the axis is $ 'r' $
If we construct a figure for the situation that is given

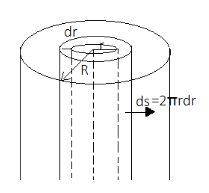
Now, as we know that the flux of the field is given by
 $ \phi = \dfrac{{{q_{net}}}}{{{\varepsilon _0}}} $
Where flux is the surface integral of an electric field.
Now, it is given that the field that is coming out of the cylinder is equal to zero, i.e.,
This implies from the formula given for the field, that the flux is also zero for this field
Then, we can see that,
 $ {q_{net}} = 0 $
The formula for the net charge of a conductor is given by
 $ {q_{net}} = \int\limits_0^R {\rho ds\, = 0} $
Putting the values for the charge density and the small area element, we get
 $ {q_{net}} = \int\limits_0^R {\left( {ar + b{r^2}} \right)2\pi rdr = 0} $
Solving this on, we get
 $ {q_{net}} = \int\limits_0^R {\left( {a{r^2} + b{r^3}} \right)dr = 0} \\
   \Rightarrow \dfrac{{a{R^3}}}{3} = - \dfrac{{b{R^4}}}{4} \\
   \Rightarrow \dfrac{a}{b} = - \dfrac{{3R}}{4} \\ $
Hence, the ratio of $ a $ and $ b $ i.e. $ \dfrac{a}{b} $ is $ - \dfrac{{3R}}{4} $
Hence, option $ \left( C \right) - \dfrac{{3R}}{4} $ is the correct answer.

Note :
When the electric field coming out of an infinite cylinder is zero, then it implies that the flux of the field of that cylinder is also zero. Now the zero flux implies that the total net charge stored inside the conductor is also zero. These implications are important in this question to get the ratio.