Question

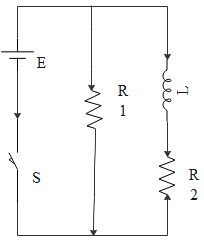
An inductor of inductance L= 400mH and resistors ${{R}_{1}}=2\Omega $ and ${{R}_{2}}=2\Omega $ are connected to a battery of emf 12V as shown in figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is:

Answer 1

Hint: Voltage across the inductor in the circuit is proportional to the rate of current flow through the inductor. For this first calculate the current flowing through the branch containing L and ${{R}_{2}}$. Then differentiate current i with respect to time t. Then using the concept voltage across an inductor is proportional to the rate of change of the current through the inductor to calculate voltage across the inductor.
Formula used:
$i=\dfrac{E}{{{R}_{2}}}\left( 1-{{e}^{\dfrac{-{{R}_{2}}t}{L}}} \right)$
where, i is the current across the inductor
E is the emf of the battery
R is the resistance
t is the time
and L is the inductance.

Complete answer:
Given that,
L=400mH
${{R}_{1}}=2\Omega $
${{R}_{2}}=2\Omega $
E= 12V
In the branch containing L and ${{R}_{2}}$,
$i=\dfrac{E}{{{R}_{2}}}\left( 1-{{e}^{\dfrac{-{{R}_{2}}t}{L}}} \right)$
Differentiating current, i with respect to time t we get,
$\Rightarrow $ $\dfrac{di}{dt}=\dfrac{E}{{{R}_{2}}}{{e}^{\dfrac{-{{R}_{2}}t}{L}}}.\dfrac{{{R}_{2}}}{L}=\dfrac{E}{L}{{e}^{\dfrac{-{{R}_{_{2}}}t}{L}}}$
Therefore,
${{V}_{L}}=L\dfrac{di}{dt}=E{{e}^{\dfrac{-{{R}_{2}}t}{L}}}$ = 12 ${{e}^{\dfrac{-2t}{400\times {{10}^{-3}}}}}$ = 12${{e}^{-5t}}V$
Then the potential drop across L as a function of time is 12${{e}^{-5t}}V$.

Additional Information:
Voltage across the inductor in the circuit is proportional to the rate of current flow through the inductor. If a current flows in an inductor, then $\dfrac{di}{dt}=0$. There is zero voltage across the inductor. Also the voltage across the inductor in the circuit is proportional to the rate of current flow through the inductor. When the current flowing through an inductor changes, the magnetic field induces an electromotive force in the conductor, known as Faraday's law of induction. According to Lenz's law, the induced voltage features a polarity (direction) which opposes the change in current that created it. The voltage across an inductor is proportional to the speed of change of the present through the inductor. Since the present source provides a continuing current, the speed of change, or slope, of the present is 0. The current level increases as the inductor stores more energy. Note that this is often precisely the other of capacitor behavior, where the storage of energy leads to an increased voltage across the component.

Note:
Voltage across the inductor in the circuit is proportional to the rate of current flow through the inductor. If a current flows in an inductor, then $\dfrac{di}{dt}=0$. There is zero voltage across the inductor. Also Voltage across the inductor in the circuit is proportional to the rate of current flow through the inductor and the constant of proportionality is the inductance.