Question

An inductive circuit contains resistance of 10Ω and an inductance of 2H. If an AC voltage of 120 Volts and frequency 60 Hz is applied to the circuit, the current would be nearly,
\[
  {\text{A}}{\text{. 0}}{\text{.32 Amp}} \\
  {\text{B}}{\text{. 0}}{\text{.16 Amp}} \\
  {\text{C}}{\text{. 0}}{\text{.48 Amp}} \\
  {\text{D}}{\text{. 0}}{\text{.80 Amp}} \\
\]

Answer 1

Hint: In order to find the magnitude of current, we observe the given data in the question (i.e. resistance, inductance, voltage and frequency are given) meaning it is a “RLC Circuit”. It is an electrical circuit which has a resistor, a capacitor and an inductor. Then we apply the formulae of the RLC circuit to find the answer.

Formula Used:
In an RLC circuit –
${\text{I = }}\dfrac{{\text{V}}}{{\text{Z}}}$, where I is the current, V is the voltage and Z is the impedance.

Complete Step-by-Step solution:
Given Data,
In the circuit, Resistance R = 10Ω
Inductance L = 2H
Voltage V = 120V
Frequency f = 60 Hz
Also,
${\text{Z = }}\sqrt {{{\text{R}}^2} + {{\text{X}}_{\text{L}}}^2} {\text{ and }}{{\text{X}}_{\text{L}}} = 2\pi {\text{fL}}$, where R is the resistance, ${{\text{X}}_{\text{L}}}$ is the reactance, f is the frequency and L is the inductance.
In an electrical circuit, impedance is defined as the measure of opposition the circuit presents to a current when voltage is applied to it.
Here we determine the impedance first and then determine the current using it.
Impedance in a RLC circuit is given as${\text{Z = }}\sqrt {{{\text{R}}^2} + {{\text{X}}_{\text{L}}}^2} $, where R is the resistance and ${{\text{X}}_{\text{L}}}$ is the reactance.
Reactance in an electrical circuit is defined as opposition of an element in the circuit, to the flow of current due to the element’s inductance or capacitance. It is given by ${{\text{X}}_{\text{L}}} = 2\pi {\text{fL}}$ where f is the frequency and L is the inductance.
Now in this circuit ${{\text{X}}_{\text{L}}} = 2\pi {\text{fL}}$
$
   \Rightarrow {{\text{X}}_{\text{L}}} = 2\pi \times 60 \times 2 \\
   \Rightarrow {{\text{X}}_{\text{L}}} = 240\pi {\text{ }}\Omega \\
$
Therefore Impedance ${\text{Z = }}\sqrt {{{\text{R}}^2} + {{\text{X}}_{\text{L}}}^2} $becomes
$
   \Rightarrow {\text{Z = }}\sqrt {{{10}^2} + {{\left( {240\pi } \right)}^2}} \\
   \Rightarrow {\text{Z = 753}}{\text{.66 }}\Omega \\
$ (π = 3.14)

Now the current in this circuit is given by ${\text{I = }}\dfrac{{\text{V}}}{{\text{Z}}}$
$
   \Rightarrow {\text{I = }}\dfrac{{120}}{{753.66}} \\
   \Rightarrow {\text{I = 0}}{\text{.159 Amp}} \\
$
Hence the current would be nearly 0.16 Amp.
Option B is the correct answer.

Note – In order to answer this type of question the key is to know the concept of an RLC circuit and the formula relevant to it. The circuit diagram of an RLC circuit looks like:

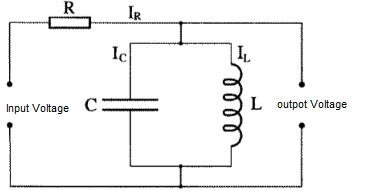
As shown it has a resistor, capacitor and an inductor with respective currents coming from each of them. When an AC current is given to the circuit the current and voltage do not necessarily have their peaks at the same instance, the fraction of their period difference between their peaks is expressed in degrees and is said to be the phase difference.
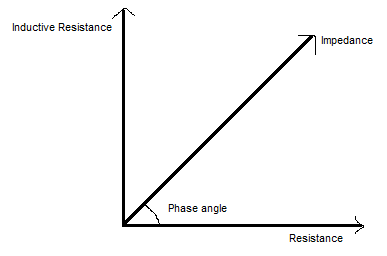
Graphically it is given as: (in terms of impedance)