Question

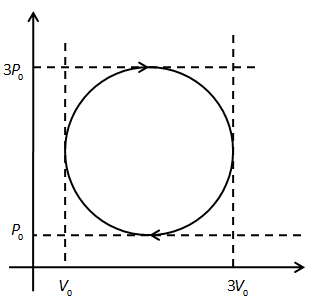
An ideal gas undergoes a circular cycle as shown in the figure. Find the ratio of maximum temperature of cycle to minimum temperature of cycle.

A. \[{\left( {\dfrac{{1 + \sqrt 2 }}{{\sqrt 2 - 1}}} \right)^2}\]
B. \[{\left( {\dfrac{{2 + \sqrt 2 }}{{2 - \sqrt 2 }}} \right)^2}\]
C. \[{\left( {\dfrac{{3 + \sqrt 2 }}{{3 - \sqrt 2 }}} \right)^2}\]
D. \[{\left( {\dfrac{{4 + \sqrt 2 }}{{4 - \sqrt 2 }}} \right)^2}\]

Answer 1

Hint: Use Ideal gas equation to express the temperature. The temperature will be a maximum when the product PV is the maximum and vice versa. Find the coordinates of the point of maximum and minimum temperature and take the ratio of it.

Complete step by step answer:According to the ideal gas equation, the product of pressure and volume is proportional to the temperature of the gas.
\[PV = nRT\]

Here, n is the number of moles of a gas and R is the gas constant.

Therefore, the temperature will be a maximum when the product \[PV\] is a maximum.

The product \[PV\] is the maximum, when the pressure and volume have the same values. We can show the points of maximum and minimum temperature in the figure below.

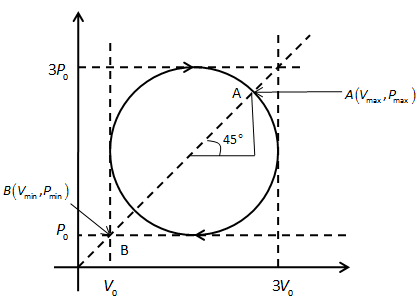
In the above figure, point A and B shows maximum and minimum temperatures respectively.
We see the radius of the circular path is \[{V_0}\] or \[{P_0}\].
We can calculate the x coordinate of point A as follows,
\[2{V_0} + {V_0}\cos 45^\circ = 2{V_0} + \dfrac{{{V_0}}}{{\sqrt 2 }}\]

And y coordinate of point A will be,
 \[2{P_0} + {P_0}\sin 45^\circ = 2{P_0} + \dfrac{{{P_0}}}{{\sqrt 2 }}\]

Therefore, the coordinates of point A are, \[A\left( {2{V_0} + \dfrac{{{V_0}}}{{\sqrt 2 }},\,2{P_0} + \dfrac{{{P_0}}}{{\sqrt 2 }}} \right)\].
Also, the coordinates of point B are, \[B\left( {2{V_0} - \dfrac{{{V_0}}}{{\sqrt 2 }},\,2{P_0} - \dfrac{{{P_0}}}{{\sqrt 2 }}} \right)\]

According to ideal gas equation, the temperature of the gas is,
\[T = \dfrac{{PV}}{{nR}}\]

Therefore, the maximum temperature of the gas is,
 \[{T_{\max }} = \dfrac{{{P_{\max }}{V_{\max }}}}{{nR}}\]
\[ \Rightarrow {T_{\max }} = \dfrac{{\left( {2{V_0} + \dfrac{{{V_0}}}{{\sqrt 2 }}} \right)\left( {\,2{P_0} + \dfrac{{{P_0}}}{{\sqrt 2 }}} \right)}}{{nR}}\]

Similarly, the minimum temperature of the gas is,
\[{T_{\min }} = \dfrac{{{P_{\min }}{V_{\min }}}}{{nR}}\]
\[ \Rightarrow {T_{\min }} = \dfrac{{\left( {2{V_0} - \dfrac{{{V_0}}}{{\sqrt 2 }}} \right)\left( {\,2{P_0} - \dfrac{{{P_0}}}{{\sqrt 2 }}} \right)}}{{nR}}\]

Now, we can take the ratio of maximum temperature \[{T_{\max }}\] and minimum temperature \[{T_{\min }}\] as follows,
\[\dfrac{{{T_{\max }}}}{{{T_{\min }}}} = \dfrac{{\dfrac{{\left( {2{V_0} + \dfrac{{{V_0}}}{{\sqrt 2 }}} \right)\left( {\,2{P_0} + \dfrac{{{P_0}}}{{\sqrt 2 }}} \right)}}{{nR}}}}{{\dfrac{{\left( {2{V_0} - \dfrac{{{V_0}}}{{\sqrt 2 }}} \right)\left( {\,2{P_0} - \dfrac{{{P_0}}}{{\sqrt 2 }}} \right)}}{{nR}}}}\]
\[ \Rightarrow \dfrac{{{T_{\max }}}}{{{T_{\min }}}} = \dfrac{{\left( {2{V_0} + \dfrac{{{V_0}}}{{\sqrt 2 }}} \right)\left( {\,2{P_0} + \dfrac{{{P_0}}}{{\sqrt 2 }}} \right)}}{{\left( {2{V_0} - \dfrac{{{V_0}}}{{\sqrt 2 }}} \right)\left( {\,2{P_0} - \dfrac{{{P_0}}}{{\sqrt 2 }}} \right)}}\]
\[ \Rightarrow \dfrac{{{T_{\max }}}}{{{T_{\min }}}} = \dfrac{{\left( {2 + \dfrac{1}{{\sqrt 2 }}} \right)\left( {\,2 + \dfrac{1}{{\sqrt 2 }}} \right)}}{{\left( {2 - \dfrac{1}{{\sqrt 2 }}} \right)\left( {\,2 - \dfrac{1}{{\sqrt 2 }}} \right)}}\]
\[ \Rightarrow \dfrac{{{T_{\max }}}}{{{T_{\min }}}} = \dfrac{{{{\left( {2\sqrt 2 + 1} \right)}^2}}}{{{{\left( {2\sqrt 2 - 1} \right)}^2}}}\]

Multiply the numerator and denominator by \[\sqrt 2 \], we get,
 \[\dfrac{{{T_{\max }}}}{{{T_{\min }}}} = \dfrac{{{{\left( {4 + \sqrt 2 } \right)}^2}}}{{{{\left( {4 - \sqrt 2 } \right)}^2}}}\]

So, the correct answer is option (D).

Note:To determine the coordinates of point B that is minimum temperature, the distance \[\dfrac{{{V_0}}}{{\sqrt 2 }}\] and \[\dfrac{{{P_0}}}{{\sqrt 2 }}\] are subtracted from the respective radius of the circular path, since the point A and B are at a same distance from the centre of the circular path. In the ideal gas equation, \[PV = nRT\], number of moles n and gas constant R is the same for both maximum and minimum temperature as we are dealing with the same gas.