Question

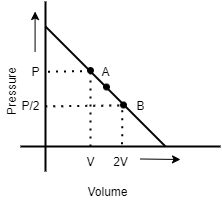
An ideal gas is taken from state \[A\] (Pressure $P$ , Volume $V$ ) to the state $B$ (Pressure $P/2$, Volume $2V$ ) along a straight line path in $PV$ diagram as shown in the adjacent figure.
Select the correct statement(s) among the following:

This question has multiple correct options:
A.the work done by the gas in the process $A$ to $B$ exceeds the work that would be done by it if the system were taken from $A$ to $B$ along the isotherm
B.in the $T - V$ diagram, the path$AB$ become part of parabola
C.in the $P - T$ diagram, the path $AB$ become part of hyperbola
D.in going from $A$ to $B$ , the temperature $T$ gas of the gas first increases to a maximum value then decreases

Answer 1

Hint:Ideal gas equation gives the relation between pressure of gas with its volume, number of moles and temperature at which the gas is present. According to the ideal gas equation pressure of gas is inversely proportional to the volume of gas and directly proportional to the temperature.
Formula used:
 $PV = nRT$
where, $P$ is the pressure, $V$ is the volume, $n$ is the number of moles, $R$ is the universal gas constant and $T$ is the temperature.

Complete step by step answer:
Here, it is given that the ideal gas from state $A$ shows pressure $ = P$
Ideal gas from state $A$ shows volume $ = V$
Ideal gas from state $B$ shows pressure $ = P/2$
Ideal gas from state $B$ shows volume $ = 2V$
As we know, the area under the $P - V$ graph is used to calculate the work done. The slope of an isothermal process is steeper than the slope of the given process. Therefore, the area under the isothermal process is less than the area under the given process.
Therefore, the work of a given process is greater than the isothermal process.
Hence, option (A) is correct.
In the given process, $P - V$ equation shows a straight line with positive intercept and negative slope.
The equation can be written as:
$P = - aV + b$
where, $P$ is the pressure, $V$ is the volume, and $a$ and $b$ are positive constants.
Now, multiplying this equation by $V$
 $PV = - a{V^2} + bV$
As we know, $PV = nRT$
This is an ideal gas equation, where $P$ is the pressure, $V$ is the volume, $n$ is the number of moles, $R$ is the universal gas constant and $T$ is the temperature.
Now, we will substitute the value of $PV$ in the above equation and we will get the following expression:
 $nRT = - a{V^2} + bV$
 $T = \dfrac{1}{{nR}}\left( { - a{V^2} + bV} \right)$
This equation is of parabola; therefore, the option (B) is correct.
Now, as from the above equation we will get the following expression:
  $T = \dfrac{1}{{nR}}\left( { - a{V^2} + bV} \right)$
As we can write:
 $\dfrac{{dT}}{{dV}} = 0$
On differentiate the equation both sides with respect to volume we will get:
 $ \Rightarrow \dfrac{1}{{nR}}\left( { - 2aV + b} \right) = 0$
 $ \Rightarrow - 2aV + b = 0$
 $ \Rightarrow V = \dfrac{b}{{2a}}$
On again differentiating it with respect to volume we will get:
Now, $\dfrac{{{d^2}T}}{{d{V^2}}} = - 2a$ , which is negative.
Hence, $T$ has maximum value. As we know that temperature is directly proportional to $PV$ from the ideal gas equation.
 $T \propto PV$
Therefore, ${(PV)_A} = {(PV)_B}$
Hence, ${T_A} = {T_B}$ .
From this, we conclude that temperatures are the same at $A$ and $B$ , but the temperature value becomes maximum in between. Therefore, going from $A$ to $B$ , the temperature of a gas first increases to a maximum value and then decreases. Thus, option (D) is also correct.
Hence, correct options are (A), (B) and (D).

Note:
-Here, the $P - V$ equation shows a straight line with positive intercept and negative slope.
$P = - aV + b$
-Work done is equal to the area under the $P - V$ graph.