Question

An ideal gas is expanded from (${p_1}$, ${V_1}$, ${T_1}$) to (${p_2}$, ${V_2}$, ${T_2}$) under different conditions. The correct statement(s) among the following is(are):
A. The work done on the gas is maximum when it is compressed irreversibly from (${p_2}$, ${V_2}$).to (${p_1}$, ${V_1}$) against constant pressure ${p_1}$.
B. The work done by the gas is less when it is expanded reversibly from ${V_1}$ to ${V_2}$ under adiabatic conditions as compared to that when expanded reversibly from ${V_1}$ to ${V_2}$ under isothermal conditions.
C. If the expansion is carried out freely, it is simultaneously both isothermal as well as adiabatic.
D. The change in internal energy of the gas is (i) zero, if it is expanded reversibly with ${T_1} = {T_2}$, and (ii) positive, if it is expanded reversibly under adiabatic conditions with ${T_1} \ne {T_2}$.

Answer 1

Hint: An isothermal condition means that the temperature of the system is constant.
An adiabatic condition means that the heat of the system is constant.

Complete step by step answer:
Step 1:
An ideal gas is expanded from (${p_1}$, ${V_1}$, ${T_1}$) to (${p_2}$, ${V_2}$, ${T_2}$) under different conditions.
During reversible expansion of an ideal gas, work done is greater than the work during an irreversible expansion of gas.
During compression, things get reversed. Thus, in reversible compression, work done is smaller.
In irreversible compression, more work is needed to be done on the gas to compress the gas. Thus, the work done in an irreversible compression is maximum.
Thus, the statement ‘work done on the gas is maximum when it is compressed irreversibly from (${p_2}$, ${V_2}$).to (${p_1}$, ${V_1}$) against constant pressure ${p_1}$’ is correct.
Step 2:
An ideal gas is expanded reversibly under adiabatic condition:
An adiabatic condition means that the change in heat of the system is constant. For an adiabatic reversible expansion,
$P{V^\gamma } = {\text{Constant}}$
Thus, as the pressure of the gas increases, the volume of the gas decreases steeply.
An ideal gas is expanded reversibly under isothermal condition:
An isothermal condition means that the change in the temperature of the system is constant. For an isothermal reversible expansion,
$PV = {\text{Constant}}$ (Boyle’s law)
Thus, as the pressure of the gas increases, the volume of the gas decreases but not very steeply.
The plot of pressure v/s volume for adiabatic and isothermal reversible expansion is as follows:

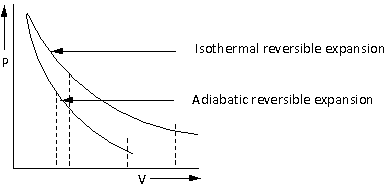
The area under the curve is the work done. From the plot, the work done during an adiabatic reversible expansion of gas is less than the work done during an isothermal reversible expansion of gas.
Thus, the statement ‘the work done by the gas is less when it is expanded reversibly from ${V_1}$ to ${V_2}$ under adiabatic conditions as compared to that when expanded reversibly from ${V_1}$ to ${V_2}$ under isothermal conditions’ is correct.
Step 3:
When an ideal gas expands freely, the following conditions are observed:
The external pressure on the gas is zero $({P_{{\text{external}}}} = 0)$.
The work done during the free expansion is zero $(W = 0)$.
The change in internal energy of the system is zero $(\Delta U = 0)$.
The change in the heat of the system is zero $(q = 0)$.
When an ideal gas expands, $\Delta U = 0$. When the change in internal energy is zero, the change in temperature is zero and the process is isothermal (Joule’s law). Thus, when an ideal gas expands freely, the process is isothermal as well as adiabatic.
Thus, the statement ‘if the expansion is carried out freely, it is simultaneously both isothermal as well as adiabatic’ is correct.
Step 4:
When ${T_1} = {T_2}$, the change in temperature is zero $(\Delta T = 0)$. Thus, the process is isothermal.
For an isothermal process, the change is internal energy is zero.
When the condition is adiabatic, no external heat is supplied to the system. Thus, for an ideal gas to expand, the gas molecules absorb the energy of the system.
Thus, the internal energy of the system decreases and the change in the internal energy of the system becomes negative.
Thus, the statement ‘the change in internal energy of the gas is (i) zero, if it is expanded reversibly with ${T_1} = {T_2}$, and (ii) positive, if it is expanded reversibly under adiabatic conditions with ${T_1} \ne {T_2}$’ is incorrect.
Thus, the correct options are option (A), option (B) and option (C).

Note:
-Boyle’s law states that the pressure of a gas is inversely proportional to the volume of the gas at a constant temperature.
-Joule’s law states that the internal energy of an ideal gas depends only on the temperature of the gas and is independent of its volume and pressure.