Question

An ideal gas goes from state A to state B via three different processes as indicated in the P-V diagram.

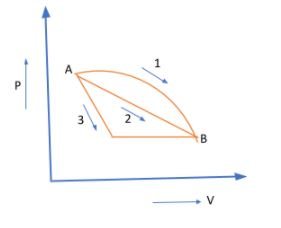
If $Q_1,Q_2,Q_3$ indicate the heat absorbed by the gas along the three processes and $\Delta U_1, \Delta U_2, \Delta U_3$ indicate the change in internal energy along the three processed respectively, then:
A. $Q_3 > Q_2 > Q_1$ and $\Delta U_1 = \Delta U_2 = \Delta U_3$
B. $Q_1 = Q_2 = Q_3$ and $\Delta U_1 > \Delta U_2 > \Delta U_3$
C. $Q_3 > Q_2 > Q_1$ and $\Delta U_1 > \Delta U_2 > \Delta U_3$
D. $Q_1 > Q_2 > Q_3$ and $\Delta U_1 = \Delta U_2 = \Delta U_3$

Answer 1

Hint: Think of the first law of thermodynamics and how you would quantify it using heat and internal energy. Also, remember that internal energy is path independent and depends only on the initial and final states for different processes whereas work done is path dependent and varies accordingly.

Formula used:
First law of thermodynamics: $Q = W + \Delta U$ where,
$Q$ is the heat absorbed by the gas, $W$ is the thermodynamic work done by the gas and $\Delta U$ denoted the change in the internal energy of the gas.

Complete step-by-step answer:
Let us attempt to deconstruct the question and understand what these thermodynamic processes entail.
Since the question requires us to establish a relation between $Q$ and $\Delta U$ we can utilize the quantifiable form of the first law of thermodynamics.
The first law of thermodynamics applies the principle of conservation of energy to systems that contain heat transfer processes and work, contributing to the transfer of energy in and out of the system. Quantitatively it describes the net heat transfer as the sum of amount of work done and the change in internal energy of the system’s constituents. It is given as :
$Q = W + \Delta U$ where,
$Q$ is the heat absorbed by the gas, $W$ is the thermodynamic work done by the gas and $\Delta U$ denoted the change in the internal energy of the gas.
The internal energy of the gas can be thought of as the sum of all kinetic energies of individual gas molecules. Therefore, change in internal energy is path independent and depends only on the initial and final states.
Therefore, for all the three processes in the P-V diagram, the change in internal energy is the same since all the processes undergo a state change from $A \rightarrow B$, i.e.,
$\Delta U_1 = \Delta U_2 = \Delta U_3$
Now, from the first law of thermodynamics we have already defined that the heat absorbed $Q = W + \Delta U$.
Since we’ve established the $\Delta U$ is the same for all three processes we now try to determine the dependency of $Q$ on $W$.
We can say that for any process the work done is given by
$W = F \Delta S$ where $\Delta S$ is the change in its path.
$\Rightarrow W = (P A) \Delta S$ since Pressure $P = \dfrac{Force}{Area} \Rightarrow F = PA$
$\Rightarrow W = P (A \Delta S)$ where $(A \Delta S)$ is basically change in volume
$\Rightarrow W = P \Delta V$
If we look at the P-V diagram we can see that by finding $ P \Delta V $ which is just the area under the curve, we can determine the work done by the gas in the three processes and hence determine corresponding $Qs$.
Evidently, the $Area_{1} > Area_{2} > Area_{3}$. This means that
$W_1 > W_2 > W_3$
Revisiting the first law: $Q = W + \Delta U$
Since $W_1 > W_2 > W_3$ and $\Delta U_1 = \Delta U_2 = \Delta U_3$
$\Rightarrow Q_1 > Q_2 > Q_3$.

So, the correct answer is “Option D”.

Note: Remember to be careful with the signs, since work done “by” the gas is different from work done “on” the gas. In the above discussion we’ve carried out our analysis in the perspective of work done “by” the gas, i.e. $W_{by gas} = -\; W_{on gas }$. However, the area under the curve will still represent the magnitude of work done.
There are also two different sign conventions:
Clausius convention: $\Delta U = Q - W$, which we have used.
IUPAC convention: $\Delta U = Q - W$.
Ensure that any calculations or analysis that you do is consistent with the chosen convention.