Question

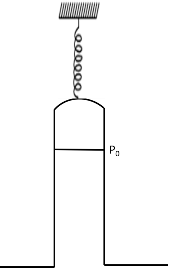
An ideal barometer tube of negligible mass is suspended from a spring balance as shown. The mass of mercury in the tube is m and atmospheric pressure is $ P_0 $ . The cross-section area of the tube is A. The reading of spring balance is:

A. \[mg\]
B. \[{P_0}A\]
C. \[{P_0}A{\text{ }} - {\text{ }}mg\]
D. $\dfrac{{{P_0}A{\text{ + }}mg}}{2}$

Answer 1

Hint: In the question, we have been asked about the reading of the spring balance of the given figure. So, to solve this question we will start with taking restoring force, kx of spring it will be equal to weight, i.e., mg. Now the fluid will also exert some force, hence on getting all the required value, we will get the required answer.

Complete step by step answer:
We have been given an ideal barometer tube of negligible mass which is suspended from a spring balance. It is given that the mass of mercury in the tube is ‘m’ and atmospheric pressure is and the cross-section area of the tube is A. We need to find the reading of spring balance.
The given mass of mercury in the barometer tube \[ = {\text{ }}m\]
The given atmospheric pressure \[ = {\text{ }}{P_0}\]
And, cross-section area of the given tube \[ = {\text{ }}A\]
Barometer tube of negligible mass is suspended from a spring balance, and we know that the spring always measures contraction of expansion depending on the nature of force acting on it.
So, when the weight is attached to the spring, the weight gets displaced from its equilibrium position and the restoring force acts on the weight. At equilibrium the only force acting will be mg.
Hence, the restoring force kx, \[kx{\text{ }} = {\text{ }}mg.\]
where, k \[ = \] spring constant
And there is a fluid inside the barometer, i.e., mercury will exert pressure inside the tube and it will raise to some height h.
So, atmospheric pressure, \[{P_0} = \rho gh\]\[ \ldots eq.\left( 1 \right)\]
\[\rho gh = \dfrac{F}{A}\]\[ \ldots .eq.\left( 2 \right)\]
where, F \[ = \] force
So, from \[eq.\left( 1 \right)\] and \[eq.\left( 2 \right),\] we get
\[F = {P_0}A\]
So, the reading of spring balance is \[{P_0}A.\]

So, the correct answer is “Option B”.

Note:
In the solution, we have mentioned, that \[kx{\text{ }} = {\text{ }}mg.\]To understand this, we will take an example, suppose on vertically hanging a mass m from a spring with spring constant k. Initially the spring will expand due to the weight attached but afterwards it will come to rest. That’s why, then kx will be equal to mg. Basically, the weight of mass will be balanced by spring force.