Question

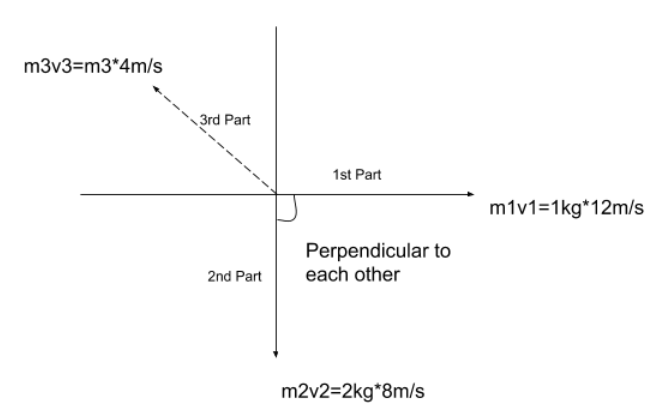
An explosion blows a rock into three parts. Two parts go off at right angles to each other. The first part weighing 1kg is moving with a velocity of $12m{s^{ - 1}}$ and the second part weighing 2 kg is moving with a velocity of $8m{s^{ - 1}}$. If the third part flies off with a velocity of $4m{s^{ - 1}}$, its mass would be-
(A). 3kg
(B). 5kg
(C). 7kg
(D). 17kg

Answer 1

Hint- We will use the formula of momentum i.e. $p = mv$ in order to find the momentum of the first rock and the second rock. Then we will find the resultant momentum which will be the momentum of the third part. Then we will find out the mass of the third part using the same formula of momentum.

Formula used: $p = mv$

Complete step-by-step answer:
The mass of the first part of rock is ${m_1} = 1kg$
The velocity of the first part of rock is ${v_1} = 12m/s$
The mass of the second part of rock is ${m_2} = 2kg$
The velocity of the second part of rock is ${v_2} = 8m/s$

Applying the law of conservation of linear momentum-
Momentum of the first part of the rock-
$\Rightarrow {p_1} = {m_1}{v_1}$
$ \Rightarrow {p_1} = 1 \times 12$
$\Rightarrow {p_1} = 12 \dfrac{kg m} {s} $
Momentum of the second part of the rock-
$\Rightarrow {p_2} = {m_2}{v_2}$
$\Rightarrow {p_2} = 2 \times 8$
$\Rightarrow {p_2} = 16 \dfrac{kg m} {s}$
So, the resultant momentum will be-
$\Rightarrow p = [ (P_1)^2+ (P_2)^2]^\dfrac{1}{2}$
$\Rightarrow p = [ (12)^2+ (16)^2]^\dfrac{1}{2}$
$\Rightarrow p = 20 \dfrac{kg m} {s}$
Now, we can say that the third part should also have the same momentum. So-
$ \Rightarrow p = {p_3}$ (where ${p_3}$ is the momentum of the third part)
Thus, the mass ${m_3}$ of the third stone will be-
$
   \Rightarrow {p_3} = {m_3}{v_3} \\
    \\
   \Rightarrow 20 = 4{m_3} \\
    \\
   \Rightarrow {m_3} = 5kg \\
$
Hence, the mass of the third stone will be 5kg.
Thus, option B is the correct option.

Note: As per the law of conservation of linear momentum: in the event that the net external force following up on a system of bodies is zero, at that point the momentum of the system stays consistent. We need to recall that the momentum of the system is conserved and not that of the individual particles.