Question

An explorer is caught in a whiteout (in which the snowfall is so thick that the ground cannot be distinguished from the sky) while returning to base camp. He was supposed to travel due north for $ 5.6km $ , but when the snow clears, he discovers that he actually travelled $ 7.8km $ at $ {50^ \circ } $ north of due east.
(a) How far and
(b) in what direction must he now travel to reach base camp?

Answer 1

Hint: To solve this question, one must have a concept of vector addition and then one can easily solve these types of questions. Here we will solve this question in two parts. In the first part we will simply draw the diagram and as per question using the vector method and in the second part simply, we will be using $ \cos \theta $ to obtain the direction and hence we got our required solution.

Complete answer:
According to the question we know that,
 $ 5.6km $ is the distance he travelled due north and let us denote by $ D $ ,
 $ 7.8km $ is the actual distance that he travelled and let us denote by $ d $ and
And also given the direction and angle that he travelled is north of due east with an angle $ {50^ \circ } $ .
Let us draw a rough diagram and proceed.

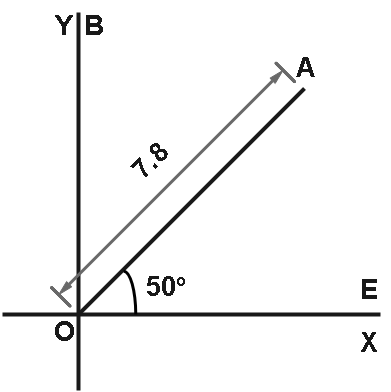
For solution part (a)
From here we can say that,
 $ \overrightarrow {OA} = 7.8\cos {50^ \circ }\hat i + 7.8\sin {50^ \circ }\hat j $
And as per the question it is given that the explorer want to travel $ 5.6\hat j $ as this is very clear from the diagram that the explorer has to travel $ A $ to $ B $ to calculate that simply we have to minus $ \overrightarrow {OB} - \overrightarrow {OA} $
 $
  \overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \\
   \Rightarrow \overrightarrow {AB} = 5.6\hat j - 7.8\cos {50^ \circ }\hat i + 7.8\sin {50^ \circ }\hat j \\
   \Rightarrow \overrightarrow {AB} = - 5.01\hat i - 0.375\hat j \\
  $
Now, we got $ \overrightarrow {AB} $ and this is in vector form and to convert we simply have to take the magnitude,
 $
  \overrightarrow {AB} = - 5.01\hat i - 0.375\hat j \\
  \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( { - 5.01} \right)}^2} + {{\left( { - 0.375} \right)}^2}} \\
   \Rightarrow \left| {\overrightarrow {AB} } \right| = 5.024 \\
  $
Hence, the explorer will have to travel $ 5.024km $ to reach the camp.
Now for solution part (b)
Here we have to calculate the direction in which he has to travel.
We know that the direction in vectors is given by $ \cos \theta $ .
 $ \therefore \theta = {\cos ^{ - 1}}\left( {\dfrac{{5.01}}{{5.024}}} \right) \\
   \Rightarrow \theta = {4.27^ \circ } \\ $
Hence, the explorer will have to travel $ 5.024km $ with an angle $ {4.27^ \circ } $ south of due west to reach the base camp.

Note:
We know that vectors consist of two-part magnitudes and other directions so we have to calculate both the parts and this is very important to note that to find the direction we use $ \cos \theta $ and this is because the solution to this question is hidden in the vector sum of two vectors.