Question

An equilateral triangle of side 9cm is inscribed in a circle. Find the radius of the circle.

Answer 1

Hint: In this question, we will start by making the diagram according to the information given in the question. The centre of the circle is the point of intersection of the perpendicular bisectors of the sides of the inscribed equilateral triangle. We will find the radius by using trigonometric ratio.

Complete step by step answer:
First we will make the diagram for the question:

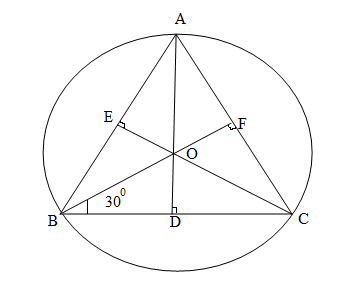
Triangle ABC is an equilateral triangle such that AB = BC = CA = 9cm.
Construction:- We have drawn perpendicular bisectors AD , BF and CE of the corresponding three sides of the triangle. ‘O’ is the point of intersection of these perpendicular bisectors.

We know that in an equilateral triangle, all sides and all angles are equal.
Measure of each angle = ${60^0}$
$\because $ AD is the perpendicular bisector of the side BC. So, we can say that:
BD = DC = 4.5cm.
We know that the perpendicular bisector divides the triangle into two congruent triangles.
 $\therefore \angle EBO = \angle DBO = \dfrac{{{{60}^0}}}{2} = {30^0}$
We have point ‘O’ which is the intersection of these perpendicular bisectors and also the centre of the circumcircle.
So, we will now find the radius of this circle using trigonometry.
$\vartriangle OBD$ is a right triangle and $\angle OBD = {30^0}$.
On applying trigonometry ratio, we get:
$\cos {30^0} = \dfrac{{BD}}{{OB}}$
$ \Rightarrow OB = \dfrac{{BD}}{{\cos {{30}^0}}}$ .
Putting the value in above equation, we get:
$ \Rightarrow OB = \dfrac{{4.5}}{{\sqrt 3 /2}} = \dfrac{9}{{1.732}}$=5.196.

Therefore, the radius of the circle = OB = 5.196cm.

Note: In this question, you should know about the circumcircle of the triangle. It is a triangle whose centre is the point of intersection of the perpendicular bisectors of the sides of the triangle and touches the vertices of the triangle. The property of the perpendicular bisectors is that it divides the side into two parts and also, it is perpendicular to it.