Question

An equilateral triangle is cut along its line of symmetry. How many isosceles triangles are formed?
A) 0
B) 1
C) 2
D) 3

Answer 1

Hint: Here first we will draw an equilateral triangle with the line of symmetry and then observe the triangles so formed whether they are isosceles triangles or not.

Complete step-by-step answer:
It is given that an equilateral triangle is cut along its line of symmetry.
Let us assume the sides AB=BC=CA=a

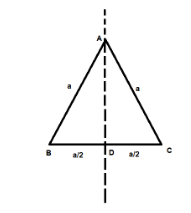
When we draw the line of symmetry which is the perpendicular bisector of the base of the equilateral triangle i.e. BC, we get two triangles as the result.
Therefore, \[\Delta ABD\] and \[\Delta ADC\] are formed as the result.
Now since AD is the perpendicular bisector of BC, therefore it divides BC into two equal parts
Hence we get:-
\[BD = DC = \dfrac{1}{2}BC\]
Hence the length of BD and CD is equal to \[\dfrac{a}{2}\]
Therefore, \[BD = DC = \dfrac{a}{2}\]
Now in \[\Delta ABD\]
\[A{B^2} = A{D^2} + B{D^2}\]
Putting in the values we get:-
\[{a^2} = A{D^2} + \dfrac{{{a^2}}}{4}\]
Solving it further we get:-
\[A{D^2} = {a^2} - \dfrac{{{a^2}}}{4}\]
Taking the LCM we get:-
\[A{D^2} = \dfrac{{4{a^2} - {a^2}}}{4}\]
\[ \Rightarrow A{D^2} = \dfrac{{3{a^2}}}{4}\]
Taking the square root we get:-
\[AD = \dfrac{{\sqrt 3 a}}{2}\]
This implies \[AB \ne BD \ne AD\]
Therefore no isosceles triangle is formed as it has two equal sides.

Hence, option A is correct.

Note: Students should note that an isosceles triangle has two sides and the two corresponding angles are equal.
Also, an equilateral triangle has three lines of symmetry.
The line of symmetry is an imaginary line on any plane which divides it into equal halves.