
An ellipse is described by using an endless string which is passed over two pins. If the axes are 6cm and 4cm, find the necessary length and distance between the pins.
(A) \[6+2\sqrt{5}\]
(B) \[6-2\sqrt{5}\]
(C) \[3+\sqrt{5}\]
(D) \[3-\sqrt{5}\]
Answer
521.1k+ views
Hint: We are given an ellipse which is made by using endless strings passed over two pins. We are given the two axes as 6cm and 4cm. We are asked to find the length of the string and also the distance between the pins. We will first find the eccentricity of the given ellipse using the formula, \[{{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right)\]. Then, we will find the foci, using the formula, \[c=ae\]. The length of the endless string is found using the expression, \[2a+2ae\] and the distance between the pins is equal to the \[ae\]. Hence, we will have the required values.
Complete step by step answer:
According to the given question, we are given an ellipse which is described using an endless string passed over two pins. The axes given to us are, 6cm and 4cm, and we are asked to find the length of the string and the distance between the pins.
We know that the standard equation of ellipse with origin as the centre is as follows,
\[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]
Here, we have,
\[2a=6\] and \[2b=4\]
So, we have,
\[a=3\] and \[b=2\]
Firstly, we will have to find the eccentricity of the given ellipse and so we will use the formula,
\[{{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right)\]
Substituting values, we get,
\[\Rightarrow {{2}^{2}}={{3}^{2}}\left( 1-{{e}^{2}} \right)\]
Solving for ‘e’, we get,
\[\Rightarrow \dfrac{4}{9}=1-{{e}^{2}}\]
\[\Rightarrow {{e}^{2}}=1-\dfrac{4}{9}=\dfrac{9-4}{9}\]
\[\Rightarrow {{e}^{2}}=\dfrac{5}{9}\]
We get the value of ‘e’ as,
\[\Rightarrow e=\dfrac{\sqrt{5}}{3}\]
We know eccentricity has another formula, which is,
\[e=\dfrac{c}{a}\]
So, we will now find the total length between the pins (which is actually the foci), we get,
\[2c=2ae=2\times 3\times \dfrac{\sqrt{5}}{3}=2\sqrt{5}\]
The length of the string will be equal to the length of the major axis, that is, we have,
\[2a=6\]
So, we have the ellipse as,
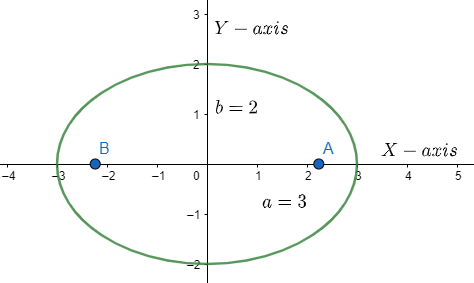
Therefore, the length of the string and distance between the pins is option (A) \[6+2\sqrt{5}\].
So, the correct answer is “Option A”.
Note: The pins are placed at the two focus of the ellipse and so to find the distance between we have to double the value of \[ae\]. The diagram of the ellipse looks like this,
Here, A and B are the positions of the pins using which the ellipse was made as strings were passed through them.
Similarly, the value of the length of the string will equal to the length of the major axis which is, \[2a\]. Do not get confused with both the terms.
Complete step by step answer:
According to the given question, we are given an ellipse which is described using an endless string passed over two pins. The axes given to us are, 6cm and 4cm, and we are asked to find the length of the string and the distance between the pins.
We know that the standard equation of ellipse with origin as the centre is as follows,
\[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]
Here, we have,
\[2a=6\] and \[2b=4\]
So, we have,
\[a=3\] and \[b=2\]
Firstly, we will have to find the eccentricity of the given ellipse and so we will use the formula,
\[{{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right)\]
Substituting values, we get,
\[\Rightarrow {{2}^{2}}={{3}^{2}}\left( 1-{{e}^{2}} \right)\]
Solving for ‘e’, we get,
\[\Rightarrow \dfrac{4}{9}=1-{{e}^{2}}\]
\[\Rightarrow {{e}^{2}}=1-\dfrac{4}{9}=\dfrac{9-4}{9}\]
\[\Rightarrow {{e}^{2}}=\dfrac{5}{9}\]
We get the value of ‘e’ as,
\[\Rightarrow e=\dfrac{\sqrt{5}}{3}\]
We know eccentricity has another formula, which is,
\[e=\dfrac{c}{a}\]
So, we will now find the total length between the pins (which is actually the foci), we get,
\[2c=2ae=2\times 3\times \dfrac{\sqrt{5}}{3}=2\sqrt{5}\]
The length of the string will be equal to the length of the major axis, that is, we have,
\[2a=6\]
So, we have the ellipse as,

Therefore, the length of the string and distance between the pins is option (A) \[6+2\sqrt{5}\].
So, the correct answer is “Option A”.
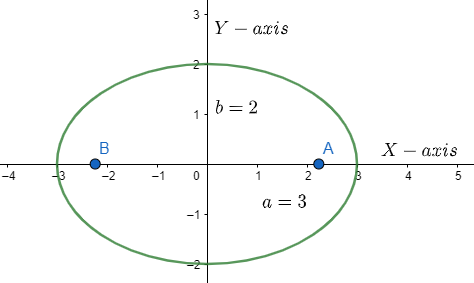
Note: The pins are placed at the two focus of the ellipse and so to find the distance between we have to double the value of \[ae\]. The diagram of the ellipse looks like this,

Here, A and B are the positions of the pins using which the ellipse was made as strings were passed through them.
Similarly, the value of the length of the string will equal to the length of the major axis which is, \[2a\]. Do not get confused with both the terms.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




