Question

An elevator car has a mass of 1600 kg and is carrying passengers having a combined mass of 200 kg. A constant friction force of 4000 N retards its motion. How much power must a motor deliver to lift the elevator car and its passengers at a constant speed of 3.00 m/s?

Answer 1

Hint:
We are given an elevator known as lift. The total mass of the lift and the elevator can be calculated. The elevator intends to move upward at some constant speed but a resistive force is hampering its motion. We can use Newton’s second law to solve this problem.

Complete Step by Step Solution:
We have drawn free body diagram of the problem
Mass of elevator= 1600 kg
Mass of passengers = 200 kg
The total mass of the lift and passengers= 1800 kg

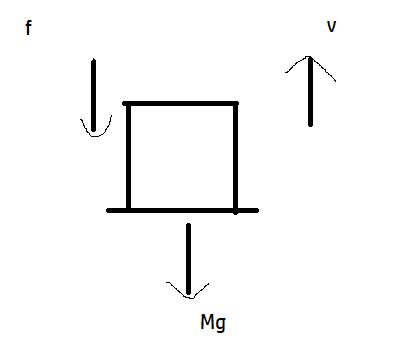
Force acting downwards= Mg
= \[1800\times 9.8=17640N\]
Frictional force acting downwards = f= 4000 N
Total downward force= 17640+4000= 21640 N
Now for a lift to move upwards tension force acts upward and since it needs to move with constant velocity, as per Newton’s second law its acceleration must be zero.
So $ T= 21640 N $
We need to calculate power and it is given by the formula P=Fv where F is the force which here is the tension.
\[
   P=Fv \\
\Rightarrow P = 21640\times 3 \\
  \Rightarrow P = 64920W \\
\]
$ \therefore $ Power needed to be delivered = $64920 W $

Note:
Here we have calculated the power using the formula P=FV, this is instantaneous power calculated by using force and velocity. This kind of problem is calculated by drawing a free body diagram and showing all the forces acting on the body.