Question

An electron having momentum $2.4 \times 10^{-23}$ kg m$s^{-1}$ enters a region of uniform magnetic field of 0.15 T. The field vector makes an angle of $30^{\circ}$ with the initial velocity vector of the electron. The radius of the helical path of the electron in the field shall be :
A. 2 mm
B. 1 mm
C. $\dfrac{\sqrt{3}}{2}$ mm
D. 0.5 mm

Answer 1

Hint: When a charged particle enters a magnetic field region (uniform), making some angle with the magnetic field direction, it is the perpendicular component of the velocity that provides circular motion to the charged particle.

Formula used:
Radius r of a particle (mass m, charge q) undergoing circular motion in a magnetic field B is given as:
$r = \dfrac{mv \sin \theta}{qB}$;
where $\theta$ is the angle that the particle velocity makes initially with the magnetic field direction.

Complete answer:
We know that when a charged particle enters a magnetic field region, with its direction of velocity being parallel to the magnetic field direction, it goes and is deflected by the magnetic field. If the particle enters making an angle of 90$^{\circ}$ with the magnetic field direction then it describes a circle.
From this we can conclude that it is the perpendicular component of the velocity that is responsible for circular motion.
We break our velocity into 2 following components:
1. $v \cos \theta$ along the magnetic field, and
2. $v \sin \theta$ perpendicular to the magnetic field.

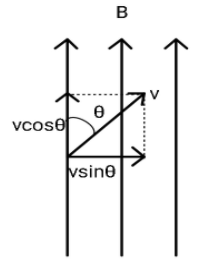
For circular motion, the centripetal force of the circular motion is equated with the Lorentz force.
$\dfrac{m(v \sin \theta)^2}{r} = q vB \sin \theta $ .
This expression will give us the radius as:
$r = \dfrac{mv \sin \theta}{qB}$
We are given the value of mv already, so upon substituting the given values, we get:
$r = \dfrac{2.4 \times 10^{-23} kg ms^{-1}}{1.6 \times 10^{-19} C \times 0.15 T \times 2 }$
$r = 5 \times 10^{-4} $m

Therefore the correct answer is option (D). The electron describes a radius of 0.5 m.

Note:
While taking the cross product, we know that for two vectors making an angle $\theta$, the magnitude of cross product is $ab \sin \theta$. Since a cross product of velocity and magnetic field is required in writing the Lorentz Force, we wrote $qvB \sin \theta$ as the magnitude of the force on the RHS side while deriving the formula.