Question

An electrician has to repair an electric fault on a pole of height 5m. He needs to reach a point 1.3m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which, when inclined at an angle of ${{60}^{o}}$to the horizontal, would enable him to reach the required position? Also, how far from the foot of the pole should he place the foot of the ladder?

Answer 1

Hint: We start solving the problem by drawing the figure representing all the given information. We find the distance between the foot of the pole and the point where electricians need to work. After drawing the given information, we use sine functions to calculate the length of the ladder that he should use. We then use tangent function to find the distance between the foot of the pole and the foot of the ladder.

Complete step-by-step answer:
Given that the electrician has to repair an electric pole of height 5m. She needs to reach 1.3m below the top of the pole to undertake the repair work. We need to find the length of the ladder that she uses to climb, when the ladder is inclined at an angle ${{60}^{o}}$to the horizontal.
Let us draw all the given information to get a better view. Let us assume the length of the ladder be y m and distance between foot of pole to foot of ladder is x m.

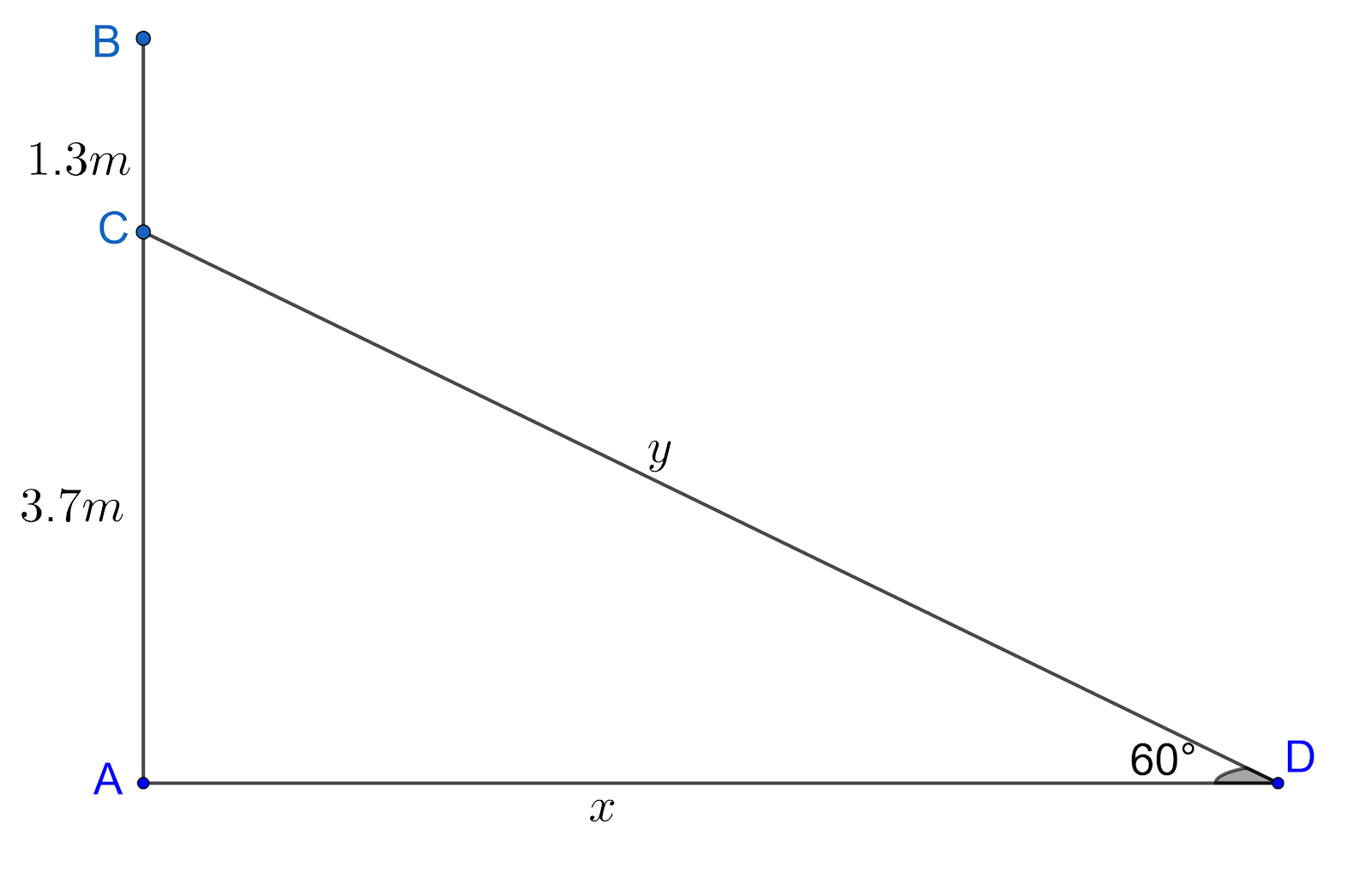
Since the height of the pole is 5m and electricians need to reach a height 1.3m less than the top point of the pole. So, an electrician needs to reach $\left( 5-1.3 \right)m=3.7m$ from the foot of the pole.
From triangle ADC, we get $\sin \left( {{60}^{o}} \right)=\dfrac{AC}{CD}$.
$\dfrac{\sqrt{3}}{2}=\dfrac{3.7}{y}$.
$y=\dfrac{3.7\times 2}{\sqrt{3}}$.
$y=\dfrac{7.4}{\sqrt{3}}m$.
∴ The length of the ladder is $\dfrac{7.4}{\sqrt{3}}m$.
From triangle ADC, we get $\tan \left( {{60}^{o}} \right)=\dfrac{AC}{AD}$.
$\sqrt{3}=\dfrac{3.7}{x}$.
$x=\dfrac{3.7}{\sqrt{3}}m$.
∴ Distance between the foot of pole and foot of ladder is $\dfrac{3.7}{\sqrt{3}}m$.
∴ Length of the ladder = $\dfrac{7.4}{\sqrt{3}}m$ and distance between foot of pole and foot of ladder = $\dfrac{3.7}{\sqrt{3}}m$.

Note: We should not connect the ladder to the top of the pole as the electrician is not intended to get to the top of the pole. Here in the problem, we took an approximation up to 2-digits in the decimal place. Here ${{60}^{o}}$ is known as angle of elevation and sometimes problems can be asked by using this name. Whenever we are asked to solve this type of problem, we should start by drawing the diagram first.