Question

An athlete completes half a c track of radius. $R$ Then the displacement and distance covered by the athlete are
A. $2R$ and $\pi R$
B. $\pi R$ and $2R$
C. $R$ and $2\pi R$
D. $2\pi R$ and $R$

Answer 1

Hint: For finishing the half-round of the circle, the separation secured will be half of the circuit of the circle. Uprooting is the briefest separation between the underlying and last positions, so the relocation will be only the breadth of the circles.

Formula used:
The sweep of the hover with edge (perimeter) is $c$$ = $$r = \dfrac{c}{{2\pi }}$
Where, $r = $radius
$c = $ Circumference
$\pi = $ Pi

Complete step by step answer:

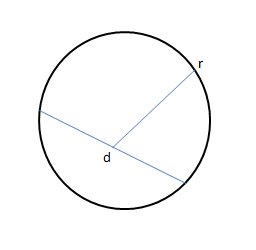
Perimeter of circular $ = R + R$
$ \Rightarrow 2R$
$ \Rightarrow 2\pi R$
Distance $ = \dfrac{1}{2} \times $ Perimeter of circular
$ \Rightarrow \dfrac{1}{2} \times 2\pi R$
$ \Rightarrow \pi R$
Displacement $ = {\rm O}{\rm A} + {\rm O}{\rm B}$
$\left( {\because OA = R,OB = R} \right)$
$ \Rightarrow R + R$
$ \Rightarrow 2R$

This article is about the line section. For the bone, see Radius (bone). For different utilizations, see Radius (disambiguation). The common condensing and numerical variable name for range. By expansion, the measurement is characterized as double the span.
If an item doesn't have a middle, the term may allude to its circumradius, the range of its encircled circle, or encompassed circle.

In either case, the sweep might be the greater part of the breadth, which is typically characterized as the most extreme separation between any two purposes of the figure. The inradius of a mathematical figure is typically the range of the biggest circle or circle contained in it.

The internal sweep of a ring, tube, or other empty article is the range of its depression. A round definition is one that utilizes the term being characterized as an aspect of the definition or expects an earlier comprehension of the term being characterized
There are a few sorts of round definitions, and a few different ways of portraying the term: logical, lexicographic, and semantic.

Hence, the correct answer is option (B).

Note: The run of the mill truncation and numerical variable name for sweep. By augmentation, the breadth is characterized as double the span.
$\dfrac{{{\text{circumference}}}}{{diameter}}$ =$\pi = 3.14159...$
The Radius is the good way from the middle outwards.
The Diameter goes straight over the hover, through the middle.
The Circumference is the separation once around the circle.