Question

An arrow is launched ${30.0^\circ }$ above the horizontal with an initial speed of $20.0m/s$ from the top of a water tower. After $3.00$ seconds, what will be the arrow's speed?
Take air resistance to be negligible and gravity to be the only source of acceleration.
(A) $19.4m/s$
(B) $20.0m/s$
(C) $26.0m/s$
(D) $29.4m/s$
(E) $34.1m/s$

Answer 1

Hint: Resolve the components of initial velocity along horizontal and vertical axes. Then find the horizontal and vertical components of final velocity. Then use the vector properties to find the magnitude of the final velocity.

Complete step by step answer:
Observe the diagram

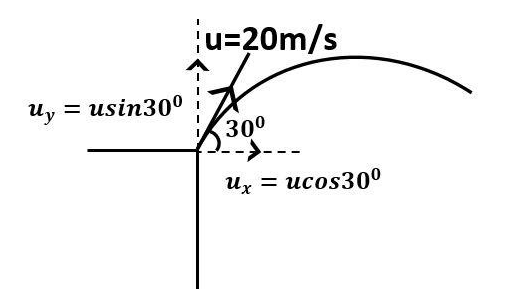
It is given in the question that,
Initial velocity of the arrow is $u = 20m/s$
The angle of projectile is $\theta = {30^0}$
We will first resolve the components of initial velocity, along the X and Y axis, respectively.
The component of initial velocity along positive X- axis will be
${u_x} = u\cos {30^0}$
$ \Rightarrow {u_x} = 20 \times \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow {u_x} = 10\sqrt 3 m/s$
The component of initial velocity along positive Y- axis will be
${u_y} = u\sin {30^0}$
$ \Rightarrow {u_y} = 20 \times \dfrac{1}{2}$
$ \Rightarrow {u_y} = 10m/s$
We have to calculate velocity after $t = 3s$
Let $v$ be the final velocity at time $t = 3s$
In projectile motion, horizontal motion occurs with constant velocity. Therefore, the horizontal component of initial and final velocity will be the same. i.e.
${v_x} = {u_x} = 10\sqrt 3 m/s$
And, the vertical component of final velocity will be affected by the constant acceleration due to gravity.
We have,
$v = u - gt$
Where,
$v$ is final velocity
$u$ is initial velocity
$g$ is acceleration due to gravity
$t$ is time period
Therefore, the vertical component of velocity can be written as
${v_y} = {u_y} - gt$
Substitute the given values in the above equation. We get
${v_y} = 10 - 10 \times 3$ $\left( {\because g = 10m/{s^2}} \right)$
$ \Rightarrow {v_y} = - 20m/s$
Now, by using the vector properties for magnitude, we can write the final velocity as
$v = \sqrt {v_x^2 + v_y^2} $
\[ \Rightarrow v = \sqrt {{{\left( {10\sqrt 3 } \right)}^2} + {{\left( { - 20} \right)}^2}} \]
$ \Rightarrow v = \sqrt {300 + 400} = \sqrt {700} $
$ \Rightarrow v = 26.45m/s$
Therefore, final velocity after $3s$ will be $v = 26.45m/s$ (approximately)

Therefore, from the above explanation, the correct answer is, option (B) $26.0m/s$

Note:You have to be very careful while applying signs to a vector quantity. You might find different ways of applying signs to such questions. In this question, we have considered the vectors along upward direction as positive and vectors along downward direction to be negative. In some other references, you might find that they have considered the vectors along upward direction to be negative and downward direction to be positive. Using any rule does not change the final answer, if you know the interpretation of the final sign that you will get.