Question

An ant leaves the anthill for its morning exercise. It walks 4 feet east and then makes a ${{160}^{\circ }}$ turn to the right and walks 4 more feet. It then makes another ${{160}^{\circ }}$ turn to the right and walks 4 more feet. If the ant continues this pattern until it reaches the anthill again, what is the distance in feet it would have walked?

Answer 1

Hint: Form the pattern of the walking of the ant and consider that the ant will form an n – sided polygon as it reaches back to the anthill. Consider that this n – sided polygon will be regular with each angle measuring ${{160}^{\circ }}$, apply the formula for the measure of each interior angles of an n – sided polygon given as $\left( \dfrac{n-2}{n} \right)\times {{180}^{\circ }}$. Solve for the value of n. Finally, multiply this value with 4 feet to get the total distance travelled by the ant.

Complete step-by-step solution:
Here we have been provided with the walking pattern of an ant and we are asked to find the total distance travelled by the ant as it reaches back it the anthill. Let us draw a pattern of the ant walking so that we can understand the situation in a better way.

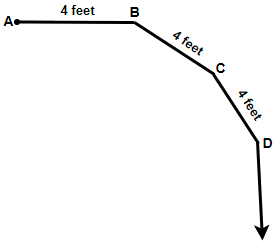
From the above pattern we can say that the ant will follow the path of a regular polygon with each angle equal to ${{160}^{\circ }}$ and the length of each side as 4 feet. Let us assume that the number of sides in the polygon is n. So applying the formula for the measure of each angle of an n – sided regular polygon given as $\left( \dfrac{n-2}{n} \right)\times {{180}^{\circ }}$ and equating it with ${{160}^{\circ }}$ we get,
$\begin{align}
  & \Rightarrow \left( \dfrac{n-2}{n} \right)\times {{180}^{\circ }}={{160}^{\circ }} \\
 & \Rightarrow \left( \dfrac{n-2}{n} \right)=\dfrac{{{160}^{\circ }}}{{{180}^{\circ }}} \\
 & \Rightarrow \left( \dfrac{n-2}{n} \right)=\dfrac{8}{9} \\
\end{align}$
By cross multiplication we get,
$\begin{align}
  & \Rightarrow 9n-18=8n \\
 & \Rightarrow 9n-8n=18 \\
 & \Rightarrow n=18 \\
\end{align}$
So, the polygon has 18 sides and each side measures 4 feet in length, therefore the sum of all the sides of the polygon will be the required distance travelled by the ant.
$\Rightarrow $ Distance travelled by the ant = $18\times 4$
$\therefore $ Distance travelled by the ant = 72 feet
Hence, the ant travels 72 feet before it reaches back to the anthill.

Note: Always remember the formula $\left( n-2 \right)\times {{180}^{\circ }}$ for the sum of interior angles of n – sided polygon. It will be beneficial for you to draw the pattern of the walk of an ant as you may get confused while imagining the path the ant is following. Remember the properties of a regular polygon regarding the measurement of its sides and angles to solve the above question.