Question

An ant is moving around a few food pieces of different shapes scattered on the floor. For which food piece would the ant have to take a longer round?

Answer 1

Hint: We will calculate the length of the boundary for each given figure. In the first figure, add the perimeter of the semicircle and the line with length 2.8cm. In figure (b), add the perimeter of the semicircle with the length of three lines as given in the figure. Then, for the figure (c), add the perimeter of the semicircle with the length of two lines as given in the figure. The figure with the maximum length of the boundary is the required answer.

Complete step by step solution: Since the ant is moving around the different shapes, the ant is covering all the boundaries of the given figures.
When we have to calculate the length of the boundary of any shape, we do it by calculating the perimeter of the shape.
Hence, we will calculate the perimeter of each given figure.
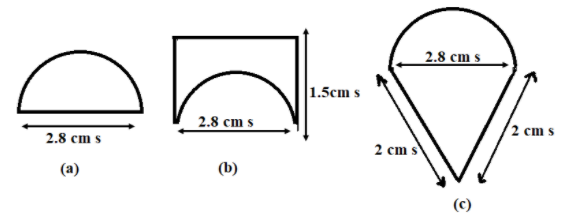
In figure (a), we can see a combination of the semicircle and a line.
First of all, we will calculate the perimeter of the semicircle.
We are given that the diameter of the semicircle is 2.8cm.
We know that radius is always half the diameter.
Hence, the radius of the given figure is,
$\dfrac{{2.8}}{2} = 1.4$
Now, the perimeter of thr semicircle is $\pi r$
On substituting \[\pi = \dfrac{{22}}{7}\] and $r = 1.4$, we get
$\dfrac{{22}}{7}\left( {1.4} \right) = 22\left( {0.2} \right) = 4.4cm$
Total perimeter of figure (a) is the sum of perimeter of the semicircle and the length of the line.
Therefore, we get the perimeter as $4.4 + 2.8 = 7.2cm$
That is, the ant has to move 7.2cm around the figure (a)
In figure (b), we have a combination of the semicircle and three lines.
The perimeter of the semicircle with radius 1.4cm, as calculated above, is 4.4cm.
The length of two lines is 1.5cm and the length of one line is 2.8cm.

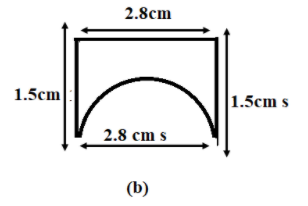
Now, the total perimeter is the sum of the perimeter of the semicircle and the length of the three lines.
Hence, the total perimeter is $4.4 + 1.5 + 1.5 + 2.8 = 10.2cm$
Therefore, the ant has to move 10.2cm around the figure (b)
Now, we will calculate the perimeter of figure (c).
In figure (c), there is a combination of the semicircle and two lines.
The perimeter of the semicircle with radius 1.4cm, as calculated above, is 4.4cm.
The length of the two lines is 2cm.
Now, the total perimeter is the sum of the perimeter of the semicircle and the length of the two lines.
Hence, the total perimeter is $4.4 + 2 + 2 = 8.2cm$
Therefore, the ant has to move 8.2cm around the figure (c)
Then, the ant will have to take a longer round in figure (b)

Note: Many students make mistakes in considering the first figure as the only semicircle. The perimeter of the semicircle, that is $\pi r$ only includes the curved part of the semicircle and not the diameter. Hence, the total perimeter of figure (a) can also be written as $\pi r + 2r$, where $r$ is the radius of the semicircle.