Question

An ant climbed 8 stairs in six minutes. Then it falls 3 stairs down in 20 seconds. Then it again tried to climb 4 more stairs in the next 2 minutes. If the width and height of each stair is $ 0.4m $ and $ 0.3m $ respectively. Then, calculate:
a) Total distance covered by the ant
b) Total displacement covered by the ant
c) Average speed and average velocity of ant

Answer 1

Hint: Distance is the total ground covered or travelled by an object whereas displacement means the length of the straight line when joining the starting and ending point of the journey of an object that has been travelling. Average speed is derived from the total distance divided by the total time elapsed but average velocity is derived from displacement. It is the displacement divided by the time elapsed.

Formula used:
For a right-angled triangle, we can write
( $ hypotenuse{e^2} = bas{e^2} + heigh{t^2} $ )
or, $ hypotenuse = \sqrt {bas{e^2} + heigh{t^2}} $
Average speed = $ \dfrac{{Total{\text{ }}distance{\text{ }}covered{\text{ }}by{\text{ an object}}}}{{Total{\text{ }}time{\text{ }}elapsed}} $
Average velocity = $ \dfrac{{Total{\text{ }}displacement{\text{ }}covered{\text{ }}by{\text{ an object}}}}{{Total{\text{ }}time{\text{ }}elapsed}} $

Complete step by step solution:
In the given problem, we have a set of stairs that we need to deal with. So at first, we need to observe a single stair and the parameters are given as follows.

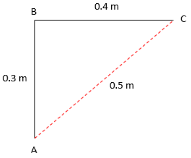
AB is the height of a single stair. BC is the width of a stair. Now, we need to calculate the distance and displacement covered by an object when climbing a stair. For a single stair,
Distance travelled = $ AB + BC = 0.3 + 0.4 = 0.7m $
Displacement = $ \sqrt {{{(AB)}^2} + {{(BC)}^2}} = \sqrt {{{(0.3)}^2} + {{(0.4)}^2}} = \sqrt {0.25} = 0.5 $
Now,the ant travelled 8 stairs up then 3 stairs down and then 4 stairs up. From this data, we can easily calculate the two important parameters.
a) Total distance covered by the ant = 8 x (Distance travelled) + 3 x (Distance travelled) + 4 x (Distance travelled) = $ (8 \times 0.7) + (3 \times 0.7) + (4 \times 0.7) = 5.6 + 2.1 + 2.8 = 10.5 $ m
b) Total displacement covered by the ant = 8 x (Distance travelled) - 3 x (Distance travelled) + 4 x (Distance travelled) = $ (8 \times 0.5) - (3 \times 0.5) + (4 \times 0.5) = 4.0 - 1.5 + 2.0 = 4.5 $ m
Now we can derive the average speed and average velocity from the above data present in (a) and (b). In order to do so, we need to have the value of total time elapsed.
Total time elapsed = 6 min + 20 sec + 2 min = $ (6 \times 60) + 20 + (2 \times 60) = 500 $ sec [ $ \because $ 1 min = 60 sec]
c) (i) Average speed = $ \dfrac{{Total{\text{ }}distance{\text{ }}covered{\text{ }}by{\text{ }}the{\text{ }}ant}}{{Total{\text{ }}time{\text{ }}elapsed}} = \dfrac{{10.5}}{{500}} = 0.021 $ m/s
(ii) Average velocity = $ \dfrac{{Total{\text{ }}displacement{\text{ }}covered{\text{ }}by{\text{ }}the{\text{ }}ant}}{{Total{\text{ }}time{\text{ }}elapsed}} = \dfrac{{4.5}}{{500}} = 0.009 $ m/s
We can conclude that,
a) Total distance covered by the ant is 10.5 m
b) ) Total displacement covered by the ant is 4.5 m
c) Average speed and average velocity of the ant is 0.021 m/s and 0.009 m/s respectively.

Note:
Displacement and distance are very different quantities. Distance is a scalar quantity and displacement is a vector quantity. Average velocity is calculated from displacement and it is also a vector quantity. Average speed is calculated from distance travelled and it is a scalar quantity.