Question

An annular ring with inner and outer radii \[{{R}_{1}}\text{ and }{{R}_{2}}\] is rolling without slipping with a uniform angular speed. The ratio of the forces experienced by the two particles situate on the inner and outer parts of the rings \[\dfrac{{{F}_{1}}}{{{F}_{2}}}\] is –
\[\begin{align}
  & \text{A) 1} \\
 & \text{B) }\dfrac{{{R}_{1}}}{{{R}_{2}}} \\
 & \text{C) }\dfrac{{{R}_{2}}}{{{R}_{1}}} \\
 & \text{D) }{{\left( \dfrac{{{R}_{1}}}{{{R}_{2}}} \right)}^{2}} \\
\end{align}\]

Answer 1

Hint: We need to understand the relation between the inner radius and outer radius of a ring with the force acting on the particles at the both parts of the ring when undergoing a rolling motion without any slipping of the ring along the motion.

Complete step by step answer:
We are given an annular ring which has inner radius as \[{{R}_{1}}\] and outer radius s \[{{R}_{2}}\]. It is given that the ring is rolling on a floor without any slipping involved in the entire motion. We are also given that the ring rolls with a uniform angular speed.
We know that for a rolling motion of a spherical body, the particles comprising the matter tend to have different linear velocities depending on their distance from the radius. A particle at the extreme end of the body will have a greater velocity as compared to the particle inside the bulk. This is in order to cover the same angular displacement in the given time.

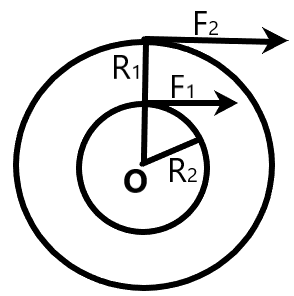
We can also understand from the above argument that, at the center of mass of the body, there will be absolutely no linear acceleration as the radius turns out to be zero.
We know the relation between the force acting on a particle and the distance of the particle from the center. Here, we need to find the force acting on particles situated at the outer surface and inner surface of the ring. The force acting on a particle is given as –
\[F=m{{\omega }^{2}}R\]
For a particle along the inner radius \[{{R}_{1}}\], the force on it is –
\[{{F}_{1}}=m{{\omega }^{2}}{{R}_{1}}\]
For a particle along the outer radius \[{{R}_{2}}\], the force on it is –
\[{{F}_{2}}=m{{\omega }^{2}}{{R}_{2}}\]
We can find the ratio between the two forces as –
\[\begin{align}
  & \dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{m{{\omega }^{2}}{{R}_{1}}}{m{{\omega }^{2}}{{R}_{2}}} \\
 & \therefore \dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{{{R}_{1}}}{{{R}_{2}}} \\
\end{align}\]
This is the required ratio between the forces acting on particles at different points in the ring.

So, the correct answer is “Option B”.

Note: For a circular body undergoing a rolling motion with a uniform angular velocity, we can consider the mass of each of the particles to be the same as we have taken in this case. The forces will be different if the mass of the particles is different in the system.