Question

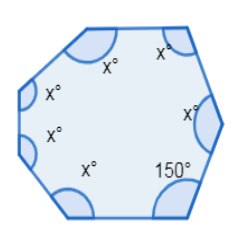
An angle of a heptagon is \[{{150}^{\circ }}\]and the other angles are \[{{x}^{\circ }}\]each. Find the value of x.

Answer 1

Hint: In this question, we first need to find the sum of interior angles in a heptagon using the formula \[\left( n-2 \right)\times {{180}^{\circ }}\]. Then equate the sum of given angles in the question accordingly and simplify further to get the result.

Complete step-by-step answer:
Now, from the given conditions in the question we have one of the angles of heptagon as \[{{150}^{\circ }}\] and all the other angles as \[{{x}^{\circ }}\]
POLYGON: Any figure bounded by three or more line segments is called a polygon.
A regular polygon is one in which all sides are equal and all angles are equal.
The name of the polygon with seven sides is heptagon
Sum of all the interior angles in a convex polygon is given by \[\left( n-2 \right)\times {{180}^{\circ }}\]
Here, n is the number of sides of a polygon.
Now, from the given conditions in the question we have
\[n=7\]
Now, let us calculate the sum of interior angles of a heptagon

\[\Rightarrow \left( n-2 \right)\times {{180}^{\circ }}\]
Now, on substituting the value of n in the above formula we get,
\[\Rightarrow \left( 7-2 \right)\times {{180}^{\circ }}\]
Now, on further simplification we get,
\[\begin{align}
  & \Rightarrow 5\times {{180}^{\circ }} \\
 & \Rightarrow {{900}^{\circ }} \\
\end{align}\]
Now, given that one angle is \[{{150}^{\circ }}\]and other 6 angles as \[{{x}^{\circ }}\]
Now, their sum can be further written as
\[\Rightarrow {{150}^{\circ }}+6{{x}^{\circ }}\]
Let us now equate this to the sum of interior angles we found above
\[\Rightarrow {{150}^{\circ }}+6{{x}^{\circ }}={{900}^{\circ }}\]
Now, on rearranging the terms we get,
\[\Rightarrow 6{{x}^{\circ }}={{750}^{\circ }}\]
Let us now divide with 6 on both sides
\[\Rightarrow {{x}^{\circ }}=\dfrac{{{750}^{\circ }}}{6}\]
Now, on further simplification we get,
\[\therefore {{x}^{\circ }}={{125}^{\circ }}\]

Note:Instead of finding the sum of interior angles separately and then equating it to the sum of given angles we can directly get it by equating them directly and simplify further.It is important to note that the given polygon is not a regular polygon so we need to find the value of x by finding the sum of interior angles. Because considering it as a regular polygon gives incorrect answers.