Question

An aluminium container of mass 100g contains 200g of ice at \[-{{20}^{0}}C\]. Heat is added to the system at a rate of 100\[cal\text{ }{{s}^{-1}}\]. What is the temperature of the system after 4 minutes? Draw a rough sketch showing the variation is the temperature of the system as a function of time. Specific heat capacity of ice \[=0.5cal\text{ }{{g}^{-1}}{{\text{ }}^{o}}{{C}^{-1}}\], specific heat capacity of aluminium \[=0.2cal\text{ }{{g}^{-1}}{{\text{ }}^{o}}{{C}^{-1}}\], specific heat capacity of water \[=1cal\text{ }{{g}^{-1}}{{\text{ }}^{o}}{{C}^{-1}}\] and latent heat of fusion of ice =\[=80cal\text{ }{{g}^{-1}}\].

Answer 1

Hint: We need to find the heat energy used in cases of lowering temperature as ice, phase transition from ice to water and the heat stored in the liquid water. We need to find the different processes that can happen within the time given.

Complete step by step solution:
We are given an aluminium container with ice in it. A heat at the rate of 100 \[cal\text{ }{{s}^{-1}}\]is provided to the system for a duration of 4 minutes. We can find the total heat energy provided to the system by using the duration as –
\[\begin{align}
  & {{H}_{total}}={{H}_{rate}}\times time \\
 & \Rightarrow {{H}_{total}}=100cal\text{ }{{\text{s}}^{-1}}\times 4\times 60s \\
 & \Rightarrow {{H}_{total}}=24000cal \\
\end{align}\]
We know that the ice at \[-{{20}^{0}}C\]lowers the temperature to \[{{0}^{0}}C\]during this time. The heat energy involved in this process can be found using the specific heat capacity of the ice and the aluminium container with the data given.
The heat of the system for temperature difference from \[-{{20}^{0}}C\] to \[{{0}^{0}}C\] is given as –
\[\begin{align}
  & {{Q}_{1}}={{Q}_{Al1}}+{{Q}_{ice1}} \\
 & \Rightarrow {{Q}_{1}}={{m}_{Al}}{{s}_{Al}}\Delta T+{{m}_{ice}}{{s}_{ice}}\Delta T \\
 & \Rightarrow {{Q}_{1}}=100g\times 0.2\times {{20}^{0}}C+200g\times 0.5\times {{20}^{0}}C \\
 & \Rightarrow {{Q}_{1}}=400cal+2000cal \\
 & \Rightarrow {{Q}_{1}}=2400cal \\
\end{align}\]
Now, we can find the heat involved the transition of ice to water at \[{{0}^{0}}C\]. The latent heat of fusion and the heat in the total mass of the ice-water system can be found as –
\[\begin{align}
  & {{Q}_{2}}={{m}_{ice}}L \\
 & \Rightarrow {{Q}_{2}}=200g\times 80cal\text{ }{{g}^{-1}} \\
 & \Rightarrow {{Q}_{2}}=16000cal \\
\end{align}\]
Now, the heat supplied is used to raise the temperature from \[{{0}^{0}}C\]to a temperature T. We can equate the total heat supplied to the sum of each heat quantities used in each step to find the temperature T as –
\[\begin{align}
  & {{H}_{total}}={{Q}_{1}}+{{Q}_{2}}+{{Q}_{3}} \\
 & \Rightarrow 24000cal=2400cal+16000cal+{{Q}_{3}} \\
 & \Rightarrow {{Q}_{3}}=24000cal-2400cal-16000cal \\
 & \Rightarrow {{Q}_{3}}=5600cal \\
\end{align}\]
The energy used to raise the temperature from \[{{0}^{0}}C\] to T can be found using the specific heat capacities of aluminium and water as –
\[\begin{align}
  & {{Q}_{3}}={{m}_{Al}}{{s}_{Al}}\Delta T+{{m}_{water}}{{s}_{water}}\Delta T \\
 & \Rightarrow {{Q}_{3}}=T(100g\times 0.2ca{{\lg }^{-1}}{{\text{ }}^{0}}{{C}^{-1}}+200g\times 1ca{{\lg }^{-1}}{{}^{0}}{{C}^{-1}}) \\
 & \Rightarrow 5600=T(20cal{{\text{ }}^{0}}{{C}^{-1}}+200cal{{\text{ }}^{0}}{{C}^{-1}}) \\
 & \Rightarrow T=\dfrac{5600}{220} \\
 & \therefore T={{25.5}^{0}}C \\
\end{align}\]
The temperature to which the ice at initially \[-{{20}^{0}}C\]is \[{{25.5}^{0}}C\]as water.
We can plot this graphically as shown below.
The time taken for each conversion is calculated by dividing the heat required for the process by the heat supply rate as –
\[\begin{align}
  & {{t}_{1}}=\dfrac{{{Q}_{1}}}{{{H}_{rate}}} \\
 & \Rightarrow {{t}_{1}}=\dfrac{2400}{100} \\
 & \therefore {{t}_{1}}=24s \\
 & \text{similarly,} \\
 & {{\text{t}}_{2}}=\dfrac{{{Q}_{2}}}{{{H}_{rate}}} \\
 & \Rightarrow {{t}_{2}}=\dfrac{16000}{100} \\
 & \therefore {{t}_{2}}=160s \\
 & \text{And,} \\
 & {{\text{t}}_{3}}=240s-{{t}_{1}}-{{t}_{2}} \\
 & \Rightarrow {{t}_{3}}=240-24-160 \\
 & \therefore {{t}_{3}}=56s \\
\end{align}\]
    

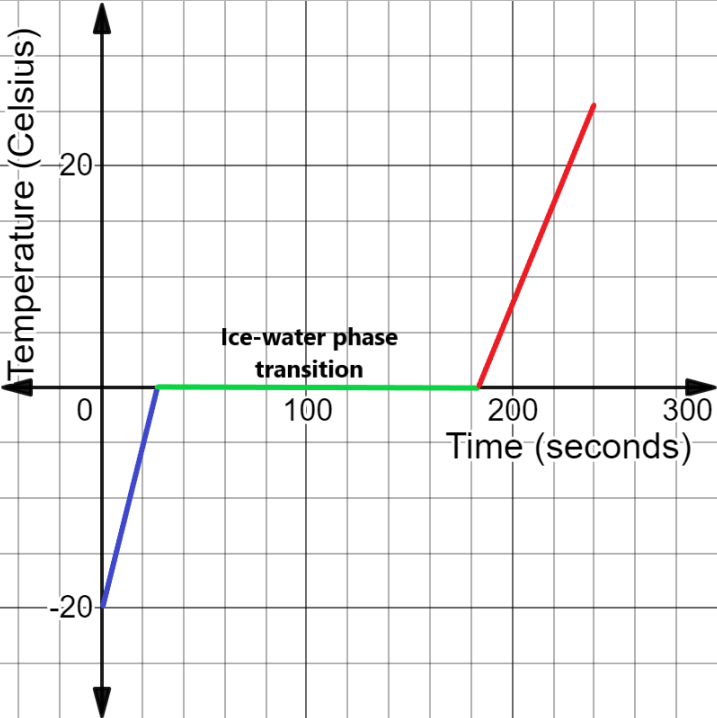
From the graph, we understand the time taken for each of the processes.

Note: We can see from the graph that the phase transition utilises a large amount of heat energy in the time interval as compared to the other processes, but there is no temperature rise. This is because the energy is used in breaking the strong forces of attraction in solid state.