Question

An altitude and a median drawn from the same vertex of a triangle divide the angle at that vertex into three equal parts. Prove that the angles of that triangle are equal to \[{{30}^{\circ }}\], \[{{60}^{\circ }}\] and \[{{90}^{\circ }}\].

Answer 1

Hint: Draw triangle ABC, let AH and AM be the altitude and median from A to base BC. Consider the triangles formed and then by applying the ASA rule, we can prove that the \[\angle BAH\] is \[{{30}^{\circ }}\], \[\angle BAM\] is \[{{60}^{\circ }}\] and \[\angle BAC\] is \[{{90}^{\circ }}\].

Complete step-by-step answer:
Let us consider ABC as the triangle. Let us draw AH as the height from A to BC which is the midpoint of the length BC. From the figure, we can say that H lies between B and M.
If we consider the \[\Delta ABH\] and \[\Delta AMH\] we can say that,

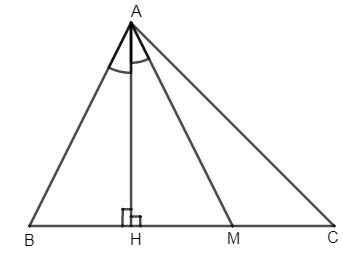
\[\angle AHB=\angle AHM\], where both are right angles.
\[\angle BAH=\angle MAH\], are equal as it is said that angles are divided equally by the altitude and median.
AH = AH, the side is common for both triangles.
Thus by ASA similarity criterion we can say that two angles and one side of \[\Delta ABH\] are equal to two angles and one side of \[\Delta AMH\]. Thus both \[\Delta ABH\] and \[\Delta AMH\] are congruent by ASA similarity criterion.
Thus we can say that, BH = HM.
\[\therefore HM=\dfrac{1}{2}BM\], from figure.
Now let us consider \[\Delta AHC\].
We said that AM is the median, but it also divides angle A into equal parts. Thus we can say that AM bisects the angle A thus we get the ratios from \[\Delta AHC\].
\[\therefore \dfrac{MH}{MC}=\dfrac{AH}{AC}\]
We said that M is the midpoint of BC. Thus we can say that, BM = CM.
We got, \[MH=\dfrac{1}{2}MB\].
Put, MB = MC.
\[\begin{align}
  & \therefore MH=\dfrac{1}{2}MC \\
 & \Rightarrow \dfrac{MH}{MC}=\dfrac{1}{2} \\
\end{align}\]
AHC is a right angles triangle at H.
\[\begin{align}
  & \Rightarrow \dfrac{MH}{MC}=\dfrac{1}{2}=\dfrac{AH}{AC} \\
 & \Rightarrow AC=2AH \\
\end{align}\]
From \[\Delta AHC\],
\[\sin C=\]opposite side / hypotenuse = \[\dfrac{AH}{AC}=\dfrac{AH}{2AH}=\dfrac{1}{2}\].
\[\begin{align}
  & \therefore \sin C=\dfrac{1}{2} \\
 & \therefore C={{\sin }^{-1}}\dfrac{1}{2}={{30}^{\circ }} \\
\end{align}\]
From trigonometric table we know that, \[\sin {{30}^{\circ }}=\dfrac{1}{2}\].
In \[\Delta AHC\], we know that \[\angle AHC={{90}^{\circ }}\] and \[\angle ACH={{30}^{\circ }}\].
We know that in a triangle, the sum of interior angles is \[{{180}^{\circ }}\].
\[\begin{align}
  & \therefore \angle HAC+\angle AHC+\angle ACH={{180}^{\circ }} \\
 & \angle HAC+{{90}^{\circ }}+{{30}^{\circ }}={{180}^{\circ }} \\
\end{align}\]
\[\Rightarrow \angle HAC=180-90-30\]
\[\Rightarrow \angle HAC=180-120={{60}^{\circ }}\]
\[\therefore \] We got, \[\angle HAC={{60}^{\circ }}\].
We got \[\Delta BAH\] and \[\angle MAH\] as congruent.

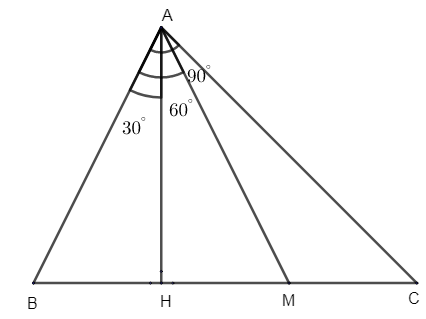
\[\therefore \angle BAH=\angle MAH=\dfrac{1}{2}\angle HAC\], from figure
\[\begin{align}
  & \therefore \angle BAH=\angle MAH=\dfrac{{{60}^{\circ }}}{2}={{30}^{\circ }} \\
 & \therefore \angle BAC=\angle BAH+\angle HAC \\
 & \therefore \angle BAC={{30}^{\circ }}+{{60}^{\circ }}={{90}^{\circ }} \\
\end{align}\]
Hence we got, \[\angle BAH={{30}^{\circ }}\], \[\angle BAM={{60}^{\circ }}\], \[\angle BAC={{90}^{\circ }}\].
Hence we proved that the angles of that triangle are equal to \[{{30}^{\circ }}\], \[{{60}^{\circ }}\] and \[{{90}^{\circ }}\].

Note: Prove the congruence of the triangles formed. To find the required angles prove that M is the midpoint of BC and H is midpoint of BM. Thus make relations connecting it. Proving the triangle will give us the proportional ratios in \[\Delta AHC\].