Question

An airplane flies on a course of $110^ \circ$ at a speed of 1200 km per hour. How far east of its starting point is it after 2h?

Answer 1

Hint: Here the given question is about the position of the airplane in which it is running, and in order to get the solution we need to plot it on figure to understand the position and hence solve the question for the position of the plane after the given time.
Formulae Used:
\[ \Rightarrow speed = \dfrac{{dis\tan ce}}{{time}}\]
\[ \Rightarrow \cos (a) = \dfrac{{adjacent}}{{hypo\tan eous}}\]

Complete step by step solution:
Plotting the given question in the figure we get:

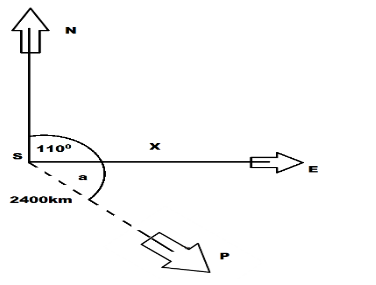
From the diagram
If the plane starts from the point S, on a bearing of 1100 and travelling at a speed of 1200km/hr, after 2 hours it will be at point P,
To find the distance from point S to point P, we get:
\[ \Rightarrow 2h \times 1200\dfrac{{km}}{h} = 2400km\]
If we are looking for the distance according to the question, due east the plane is after two hours, this is marked as point “X” on the above drawn diagram.
We can find the distance using the cosine ratio, here we first need to find the angle “a”, on solving we get:
\[ \Rightarrow \angle a = 110 - 90 = {20^ \circ }\]
Now using the cosine rule we get:
\[
   \Rightarrow \cos (a) = \dfrac{{adjacent}}{{hypo\tan eous}} = \dfrac{X}{{2400}} \\
   \Rightarrow \cos (20) = \dfrac{X}{{2400}} \\
   \Rightarrow X = 2400 \times \cos (20) = 2400 \times 0.40 = 2255.3\;km \;
 \]
Here we got the distance covered by the plane in due east direction after two hour of its journey.
So, the correct answer is “2255.3 km”.

Note: Here for the given statement question we need to first draw the associate figure as per the statement of the question, in order to solve the question we need to just think about the missing quantity like here it was distance and accordingly formulae would be used.