Question

An agricultural field is in the form of a rectangle of length 20m, width 14m. a 10m deep well of diameter 7m is dug in a corner of the field and the earth taken out of the well is spread evenly over the remaining part of the field. Find the rise in its bed.

Answer 1

Hint: We need to find the relation between the shape of the well and the earth dig out of it. We find the amount of earth and the volume of the area that has been the rise of the height of the rectangle agricultural field. We assume the height to find the volume and find a linear relation. We solve the equation to find the solution of the problem.

Complete step by step answer:
The well is of diameter 7m and is dug 10m deep. The shape of the well is of a cylinder.
The earth taken out of it has been spread evenly all-over an agricultural field in the form of a rectangle of length 20m, width 14m.
The earth in that well acts as the volume of the well. So, the volume of the well is used to make the height of the field.
Let us take the dimensions of the well.
The diameter is 7m. This means radius will be half of it. So, radius (r) = $\dfrac{7}{2}$ m.
The height of the well is $h=10$ m.

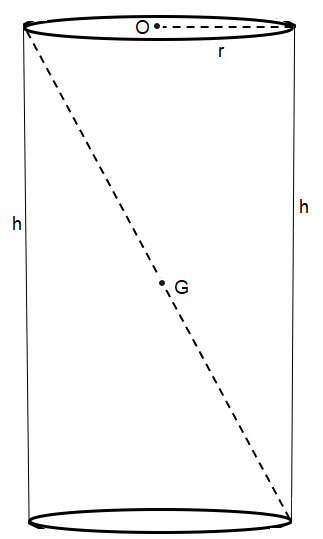
The formula of volume of a cylindrical shape is $\pi {{r}^{2}}h$.
Now we put the values to find the volume of the well which is the amount of earth.
So, volume being $V=\pi {{\left( \dfrac{7}{2} \right)}^{2}}\left( 10 \right)=\dfrac{49\times 10\times 22}{7\times 4}=385{{m}^{3}}$.
This volume of earth has been used to form a layer of earth on the agricultural field.
The volume of that rise is equal to V.
The formula for volume of a cuboid form will be $length\times breadth\times height$. Let’s assume the rise of the bed is the p unit.

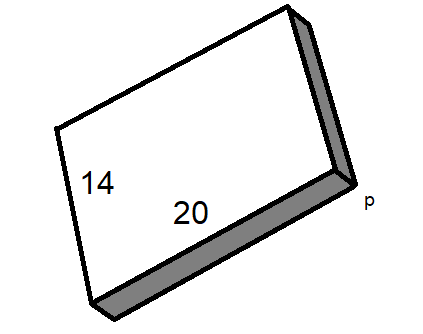
The volume of the field with the rise is $\left( 20 \right)\times \left( 14 \right)\times \left( p \right)=280p$.
We get the equation as $280p=V=385$. We solve it to get the value of p.
$\begin{align}
  & 280p=385 \\
 & \Rightarrow p=\dfrac{385}{280}=1.375 \\
\end{align}$

The height of the embankment is \[1.375m\].

Note: We need to remember that due to the rise of the height the 2d-shaped rectangle form changes into a cuboidal form. That’s why we are finding the volume, not the area. The amount of earth creates volume in both cases. So, the relation has to create a linear equation to solve the problem.