Question

An aeroplane when flying at a height of 4,000m from the ground passes vertically above another aeroplane at an instant when the angles of elevation of the two planes from the same point on the ground are ${60^ \circ }$ and ${45^ \circ }$ respectively. Find the vertical distance between the aeroplanes at that instant(take $\sqrt 3 = 1.73)$.

Answer 1

Hint: In this question first we need to find the distance between the points from which the angle of elevation of both the planes is given and the point just below both the planes on ground. Then, using this distance and properties of trigonometric angles we have to find the vertical distance between the aeroplanes at that instant.

Complete step-by-step answer:

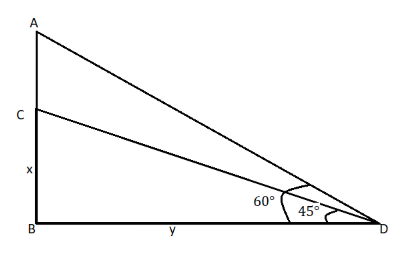
Given: An aeroplane when flying at a height of 4,000m from the ground. Let the height of the first plane be AB=4000m.
 And the angle of elevation of this plane from some point let's say D is ${60^ \circ }$. Let this angle be $\angle {\text{ADB}} = {60^ \circ }$.
Now, this first plane passes vertically above another aeroplane. Let the height of the second plane be ${\text{BC = }}x$ m.
And the angle of elevation of this plane from the same point D is ${60^ \circ }$. Let this angle be $\angle {\text{BDC}} = {45^ \circ }$.

Now, consider $\Delta {\text{CBD}}$
$
   \Rightarrow \tan {45^ \circ } = \dfrac{x}{y} \\
   \Rightarrow x = y{\text{ \{ }}\tan {45^ \circ } = 1\} {\text{ eq}}{\text{.1}} \\
 $
Now, consider $\Delta {\text{ABD}}$
$
   \Rightarrow \tan {60^ \circ } = \dfrac{{{\text{AB}}}}{{{\text{BD}}}} \\
   \Rightarrow \tan {60^ \circ } = \dfrac{{4000}}{y}{\text{ \{ AB = 4000m\} }} \\
   \Rightarrow \sqrt 3 = \dfrac{{4000}}{y}{\text{ \{ tan6}}{0^ \circ } = \sqrt 3 \} \\
   \Rightarrow y = \dfrac{{4000}}{{\sqrt 3 }} \\
   \Rightarrow y = \dfrac{{4000}}{{1.73}} \\
   \Rightarrow y = 2309.401{\text{ eq}}{\text{.2 }} \\
  {\text{ }} \\
 $
Now from eq.1 and eq.2 we get
$ \Rightarrow x = y = 2309.401$
Now, the vertical distance between the aeroplanes at that instant is given by $
   \Rightarrow 4000 - x \\
   \Rightarrow 4000 - 2309.401{\text{ \{ }}x = 2309.401\} \\
   \Rightarrow 1690.599m \\
 $
Hence, the vertical distance between the aeroplanes at that instant is 1690.599m.

Note: Whenever you get this type of question the key concept to solve is to make a figure using given information. Then using trigonometric angles properties find the required result. And remember one more thing that angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object.