Question

An aeroplane is flying horizontally at a height of 3150 m above a horizontal plane ground. At a particular instant it passes another plane vertically below it. At this instant, the angles of elevation of the planes from a point on the ground are $ 30^\circ $ and $ 60^\circ $ . Hence, the distance between the two planes at that instant is:
(A) 1050 m
(B) 2100 m
(C) 4200 m
(D) 5250 m

Answer 1

Hint: Let the required distance be $ x $ . Draw a diagram using the given information to get two right angled triangles. Call the common base as $ y $ . Use $ \tan \theta = \dfrac{{Length{\text{ }}of{\text{ }}the{\text{ }}opposite{\text{ }}side}}{{Length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}} $ to get the equations $ \tan 30^\circ = \dfrac{y}{{3150}} = \dfrac{1}{{\sqrt 3 }} $ and $ \tan 30^\circ = \dfrac{{3150 - x}}{y} = \dfrac{1}{{\sqrt 3 }} $ . Solve them to get the answer.

Complete step-by-step answer:
We are given the information about the flight of a plane.
It is flying horizontally above a horizontal ground at a height of 3150 m.
It passes another aeroplane vertically below it at some point.
At this point, the angle of elevation for the lower plane is $ 30^\circ $ and the one flying above it is $ 60^\circ $ .
Call the distance between the two planes as $ x $ .
Let’s draw a diagram using this information.
We can consider the height of the higher aeroplane from the ground as the perpendicular side of a right angled triangle.
Let the length of the base of the triangle be $ y $ m. Then we get the following picture:

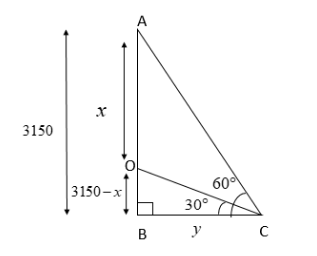
Thus, we get a right angled triangle ABC with perpendicular sides of length 3150 m and $ y $ m; and another right angled triangle OBC with perpendicular sides of length $ (3150 - x) $ m and $ y $ m.
Also, the measures of the angles of both the triangles are $ 30^\circ ,60^\circ ,90^\circ $ .
We know that in a right angled triangle, $ \tan \theta = \dfrac{{Length{\text{ }}of{\text{ }}the{\text{ }}opposite{\text{ }}side}}{{Length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}} $
In triangle ABC, $ \tan 30^\circ = \dfrac{y}{{3150}} = \dfrac{1}{{\sqrt 3 }} $ .
This implies we have $ y = \dfrac{{3150}}{{\sqrt 3 }}...(1) $
Similarly, in triangle OBC, $ \tan 30^\circ = \dfrac{{3150 - x}}{y} = \dfrac{1}{{\sqrt 3 }}.....(2) $
Therefore using (1) in (2), we get
  $
  \dfrac{{3150 - x}}{{\dfrac{{3150}}{{\sqrt 3 }}}} = \dfrac{1}{{\sqrt 3 }} \\
   \Rightarrow 3150 - x = \dfrac{1}{{\sqrt 3 }} \times \dfrac{{3150}}{{\sqrt 3 }} = \dfrac{{3150}}{3} \\
   \Rightarrow 3 \times (3150 - x) = 3150 \\
   \Rightarrow 9450 - 3x = 3150 \\
   \Rightarrow 3x = 9450 - 3150 = 6300 \\
   \Rightarrow x = 2100 \\
  $
Hence, the distance between the two planes is 2100 m.

Note: Angles above the horizontal line are called angles of elevation. If a question contains these angles, then the diagrammatic representation of the word problem will give you a right angled triangle. This will give you the first approach for solving such problems.