Question

An aeroplane is flying at a height of 3000 m. An observer finds his angle of elevation to be ${60^ \circ }$ and after 6 seconds it changes to ${45^ \circ }$. What is the speed of aeroplane?

Answer 1

Hint: We will begin by drawing the corresponding figure of the given statement. Then, we will use the value of $\tan {60^ \circ }$ to find the length of BC. Next, we will use the value of $\tan {45^ \circ }$ to determine the value of BE. Next, we will divide the distance travelled in 6 seconds by 6 to calculate the speed of the aeroplane.

Complete step-by-step answer:
We are given that aeroplane is flying at a height of 3000 m. Also, the angle of elevation is ${60^ \circ }$ but after 6 seconds, the angle of elevation is ${45^ \circ }$.
We will first draw the corresponding diagram.

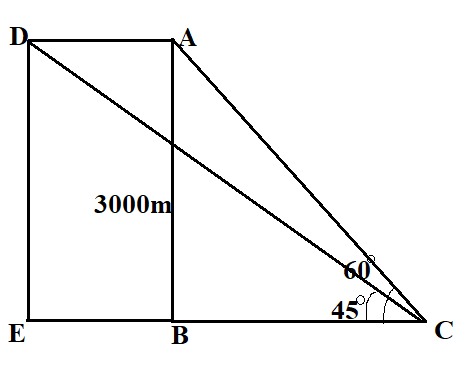
We can see, there are two triangles in the figure,
Here, the plane from point A is moved to point D in 6 seconds. The angle of elevation $\angle ACB$ changed to $\angle DCB$ after 6 seconds.
The height or perpendicular distance is the same for the triangles, DE and AB is 3000 metres.
We will now write the value of $\tan {60^ \circ }$ from the given figure, where $\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$,
$\tan {60^ \circ } = \dfrac{{AB}}{{BC}}$
We know that $\tan {60^ \circ } = \sqrt 3 $ and the value of AB is 3000 m
$
  \sqrt 3 = \dfrac{{3000}}{{BC}} \\
   \Rightarrow BC = \dfrac{{3000}}{{\sqrt 3 }} \\
   \Rightarrow BC = \dfrac{{3000}}{{1.732}} \approx 1732m \\
$
We will now find the value of $\tan {45^ \circ }$
$\tan {45^ \circ } = \dfrac{{DE}}{{BE}}$
We know that $\tan {45^ \circ } = 1$ and the value of DE is 3000 m
$
  1 = \dfrac{{3000}}{{BE}} \\
   \Rightarrow BE = \dfrac{{3000}}{1} \\
   \Rightarrow BE = 3000m \\
$
Also, $BE = BC + CE$, where $CE$ is the distance covered in 6 seconds by the plane.
$
  3000 = 1732 + CE \\
   \Rightarrow CE = 3000 - 1732 \\
   \Rightarrow CE = 1268m \\
$
Now, we know that speed is given as $\dfrac{{{\text{distance}}}}{{{\text{time}}}}$
Here, distance travelled 1268m in 6 seconds.
Therefore, speed is $\dfrac{{1268}}{6} = 211.34m/s$
Hence, the speed of the plane is 211.34 metres per second.
Note: Angle of elevation is formed when an object is above the sight of an observer. The upward angle from the point of sight is known as the angle of elevation, whereas the angle of depression is when an object is kept below the line of sight of an observer. Also, students must know how to write trigonometric ratios.