Question

An aeroplane flying in the sky with a uniform speed of 200 m/s moves in a vertical circle of radius 400 m. The mass of the pilot is 70 Kg. The force exerted by the pilot on the seat at the highest point of the circle will be
(A) 3000N
(B) 6300 N
(C) 7700 N
(D) 630 N

Answer 1

Hint:Here the aeroplane moves in a vertical circle. So, it would be quite easier if we can use the equations of the body moving in a uniform circular motion. The body experiences a force which is always directed towards the centre called centripetal force.

Complete step by step answer:
Let us draw the free body diagram representing all the forces acting on the pilot at the highest point during its motion.

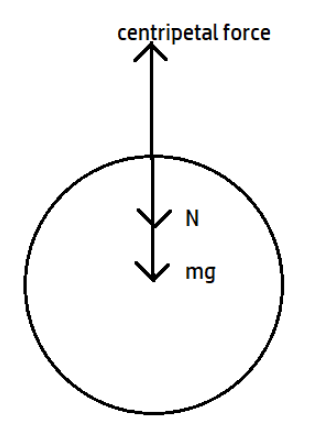
The speed of the aeroplane is 200 m/s. This is the tangential velocity of the aeroplane. The radius of the circle is 400m. The mass of the pilot is 70 kg. The aeroplane is moving in a vertical circle and we have represented the situation in FBD above. We need to find the force exerted by the pilot on the seat at the highest point of the circle. Equating the forces in the vertical direction we get,
\[\begin{align}
& \dfrac{m{{v}^{2}}}{r}=N+mg \\
&\Rightarrow N=\dfrac{m{{v}^{2}}}{r}-mg \\
&\Rightarrow N=\dfrac{70\times 200\times 200}{400}-700 \\
&\therefore N =6300N \\
\end{align}\]

So, the correct option is (B).

Note:When considering the motion in a vertical circle we need to consider the effect of gravity. The motion in a vertical circle is not uniform circular motion. Centripetal force is responsible to maintain the motion in the vertical circle.