Question

An aeroplane flying horizontally at a height of 1.5 km above the ground is observed at a certain point on earth to subtend an angle of ${60^ \circ }$. After 15 seconds, its angle of elevation is observed to be ${30^ \circ }$. Calculate the speed of the airplane in km/h.
(A). $240\sqrt 3$ $km/h$
(B). $230\sqrt 3$ $km/h $
(C). $210 $ $km/h$
(D). $220 $ $km/h$

Answer 1

Hint: To solve this question, we will develop a relationship between the height at which the aeroplane is flying and the distance covered in the horizontal direction with the help of the information given in the question.

Complete step by step solution -
In the above question, it is given that an aeroplane is flying horizontally at a height of 1.5 km from the ground. Initially, when it is observed, it was subtending an angle of ${60^ \circ }$. Now after 15 seconds, it has moved forward to some distance and the angle subtended by it is ${30^ \circ }$. Let us consider the height at which it is flying.Thus, $h = 1.5\,km\, = 1.5 \times 1000\,m$. Thus:
$h = 1500\,m$
Also, we assume that when the first time it is observed, it has already moved x meter. When it is observed the second time, it moves by meter forward. Thus, we have the following figure:

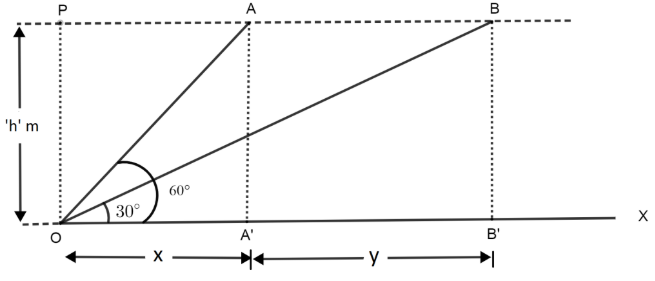
In the above figure, we can see that, originally it was at A and after 15 seconds, it moved to B. OX is the ground level, O is the observer. AA’ and BB’ are perpendiculars dropped from A and B to line OX. From the triangle OAA’, we cans say that,
$\tan \theta = \dfrac{{AA'}}{{OA'}} = \dfrac{{PO}}{{OA'}}$
$ \Rightarrow \tan {60^ \circ } = \dfrac{h}{x}$
\[ \Rightarrow x = \dfrac{h}{{\tan {{60}^ \circ }}}\]
We know that, $\dfrac{1}{{\tan {{60}^ \circ }}} = \cot \theta $. Thus, we have:
$ \Rightarrow x = h\cot {60^ \circ }$
The value of $\cot {60^ \circ } = \dfrac{1}{{\sqrt 3 }}$.Thus, we have:
$ \Rightarrow x = \dfrac{h}{{\sqrt 3 }}$ ……...……………(i)
Now, from the triangle OBB’, we can say that
$\tan {30^ \circ } = \dfrac{{BB'}}{{OB'}} = \dfrac{{PO}}{{OA' + A'B'}}$
$ \Rightarrow \tan {30^ \circ } = \dfrac{h}{{x + y}}$
$x + y = \dfrac{h}{{\tan {{30}^ \circ }}}$
$ \Rightarrow x + y = h\cot {30^ \circ }$
$ \Rightarrow x + y = h\sqrt 3 $ ……………..…………(ii)
From (i) and (ii), we can say that:
$\dfrac{h}{{\sqrt 3 }} + y = h\sqrt 3 $
$ \Rightarrow y = h\sqrt 3 - \dfrac{h}{{\sqrt 3 }}$
$ \Rightarrow y = \dfrac{{\left( {h\sqrt 3 } \right)\sqrt 3 - h}}{{\sqrt 3 }}$
$ \Rightarrow y = \dfrac{{3h - h}}{{\sqrt 3 }}$
$ \Rightarrow y = \dfrac{{2h}}{{\sqrt 3 }}$ …...……………(iii)
We know that, $h = 1500\,m$, substituting this value in above equation we get:
$\, \Rightarrow y = \dfrac{2}{{\sqrt 3 }}\, \times \,1500\,m$
$\, \Rightarrow y = \dfrac{{3000}}{{\sqrt 3 }}\,m$
Now, we know that the aeroplane covers the distance ‘y’ in 15 seconds. We know that the relation between the speed (v), distance (y) and time is given by:
$Dis\tan ce = Speed \times Time$
Let v be the velocity of the aeroplane. Thus, we get:
$\,\dfrac{{3000}}{{\sqrt 3 }}\, = v \times 15$
$\, \Rightarrow v = \dfrac{{3000}}{{\sqrt {3 \times 15} }}\,m/s\,$
$\, \Rightarrow v = \dfrac{{200}}{{\sqrt 3 }}\,m/s\,$
Now, we have to change the unit of speed into km/h. We know that $1\,km = 1000\,m$, thus $1m = \dfrac{1}{{1000}}\,km$. Also $1hr = 3600\,{\rm{seconds}}$, thus $1s = \dfrac{1}{{3600}}\,hour$. So we get:
\[v = \dfrac{{200}}{{\sqrt 3 }} \times \dfrac{{\left( {\dfrac{1}{{1000}}} \right)\,km}}{{\left( {\dfrac{1}{{3600}}} \right)\,hr}}\]
\[ \Rightarrow v = \left( {\dfrac{{200}}{{\sqrt 3 }} \times \dfrac{{3600}}{{1000}}} \right)\,km/hr\]
\[ \Rightarrow v = \dfrac{{720}}{{\sqrt 3 }}\,km/hr\]
\[ \Rightarrow v = \left( {\dfrac{{720}}{{\sqrt 3 }}\, \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}} \right)km/hr\]
\[ \Rightarrow v = \dfrac{{720\sqrt 3 }}{3}km/hr\]
\[ \Rightarrow v = 240\sqrt 3 \,km/hr\]
Hence, option (a) is correct.

Note: In solving this question, we have to consider that the height of the observer is negligible because there is no information given about the height of the observer above the ground level. If the height of the observer has been given then we would have made the necessary changes.