Question

An aeroplane flying horizontally at 750m above the ground to an elevation of \[{60^ \circ }\] . After 5 seconds the elevation is observed to be \[{30^ \circ }\]. What is the speed of the aeroplane in km/hr?

Answer 1

Hint: This question is simply related to trigonometric functions. Since the point of observation is the same we will first draw the diagram of the given situation of both the angles so given. Then we will use the trigonometric functions, especially the tan function. Then we will find the exact distance travelled by the plane in 5 seconds. Then we will use the formula of speed to find the speed of aeroplane.

Complete step by step answer:
Given that, An aeroplane flying horizontally at 750m above the ground to an elevation of \[{60^ \circ }\] . after 5 seconds the elevation is observed to be \[{30^ \circ }\]
Now the diagram can be drawn as,

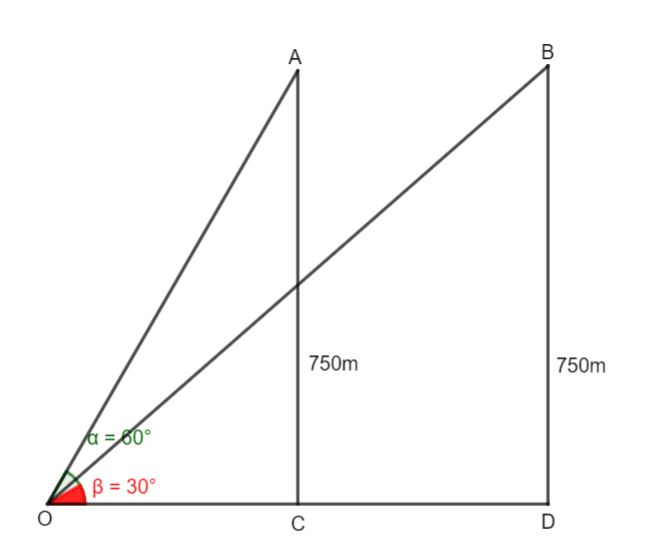
As we can see both the angles now we have to find the distance CD that the airplane has travelled in 5 seconds.
So we will consider the triangles.
In \[\vartriangle OAC\],
\[\tan {60^ \circ } = \dfrac{{AC}}{{OC}}\]
As we know that \[\tan {60^ \circ } = \sqrt 3 \] and the value of AC is the height at which the airoplane is flying.
\[\sqrt 3 = \dfrac{{750}}{{OC}}\]
\[OC = \dfrac{{750}}{{\sqrt 3 }}\]
This is the value of OC.
Now in \[\vartriangle OBD\],
\[\tan {30^ \circ } = \dfrac{{BD}}{{OD}}\]
\[\dfrac{1}{{\sqrt 3 }} = \dfrac{{750}}{{OD}}\]
\[OD = 750\sqrt 3 \]
Now, the distance it travelled in 5 seconds is given by,
\[CD = OD - OC = 750\sqrt 3 - \dfrac{{750}}{{\sqrt 3 }}\]
Taking 750 common,
\[CD = 750\left( {\sqrt 3 - \dfrac{1}{{\sqrt 3 }}} \right)\]
\[CD = 750 \times \dfrac{2}{{\sqrt 3 }}\]
This is the distance in meters but we need the distance in km,
\[CD = \dfrac{{750 \times 2}}{{1000 \times \sqrt 3 }}\]
\[CD = \dfrac{{\sqrt 3 }}{2}km\]
Now we have the distance travelled and the time taken to cover the distance so the speed can be given by,
\[speed = \dfrac{{dis\tan ce}}{{time}}\]
Since time is in seconds we will convert it in hours.
\[speed = \dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\dfrac{5}{{3600}}}}\]
\[speed = \dfrac{{\sqrt 3 \times 3600}}{{10}}\]
On simplifying we get,
\[speed = 360\sqrt 3 km/hr\]
Thus, the speed of the airplane is \[360\sqrt 3 km/hr\].

Note:
When we solve the problem the most important thing to note is what the situation actually is. Though the elevation is reduced, the height is still the same. This is the biggest mistake students generally make. Second thing to note is we are sometimes asked to find only the distance travelled but here we are about to find the speed also.
For that do observe the units always. Make them in the same measuring system either CGS or MKS or that which is asked to do.