Question

An aeroplane flying at a constant speed, parallel to the horizontal ground, \[\sqrt 3 \]km above it, is observed at an elevation of \[60^\circ \] from a point on the ground. If after five seconds, its elevation from the same point, is \[30^\circ \], then the speed (in km/hr) of the aeroplane, is
A. 1500
B. 750
C. 720
D. 1440

Answer 1

Hint: We had to only change the unit of time from seconds to hours by using formula 1 second = \[\dfrac{1}{{{\text{3600}}}}\] hours and then we had to find the distance travelled by the aeroplane in 5 seconds after that we can directly apply the speed formula which states that speed = \[\dfrac{{{\text{Distance travelled}}}}{{{\text{Time taken}}}}\] to find the speed of the aeroplane.

Complete step-by-step answer:
Let us draw the diagram from the given conditions in the question.

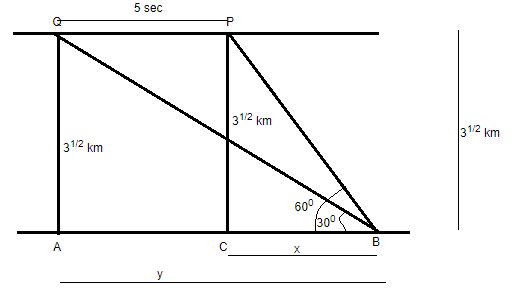
As we can see from the above figure that when the aeroplane is at point P then the angle of elevation of the aeroplane with point B at ground is equal to \[60^\circ \].
And after 5 seconds when the aeroplane is at point Q then the angle of elevation at point B on the ground is \[30^\circ \].
As seen from the above figure that the distance travelled by the aeroplane is equal to y – x.
So, we had to use trigonometric formula of \[\tan \theta = \dfrac{{{\text{Height}}}}{{{\text{Base}}}}\] to find the value of x and y.
So, in triangle PCB,
\[\tan 60^\circ = \dfrac{{PC}}{{CB}} = \dfrac{{\sqrt 3 }}{x}\] (1)
And in triangle QAB,
\[\tan 30^\circ = \dfrac{{QA}}{{AB}} = \dfrac{{\sqrt 3 }}{y}\] (2)
Now as we know that \[\tan 60^\circ = \sqrt 3 \] and \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\].
So, equation 1 becomes,
\[\sqrt 3 = \dfrac{{\sqrt 3 }}{x}\]
x = 1 km
And equation 2 becomes,
\[\dfrac{1}{{\sqrt 3 }} = \dfrac{{\sqrt 3 }}{y}\]
y = 3 km
So, the distance travelled by the aeroplane in 5 seconds is equal to y – x = 3 – 1 = 2 km.
Now we have to find the speed of the aeroplane in hours.
So, we have to change 5 seconds into hours.
As we know that 60 seconds = 1 min. So, 1 second = \[\dfrac{1}{{60}}\] minutes.
And 60 minutes = 1 hour. So, 1 minute = \[\dfrac{1}{{60}}\] hours.
So, 1 second = \[\dfrac{1}{{60}} \times \dfrac{1}{{60}} = \dfrac{1}{{3600}}\] hours.
And 5 seconds = \[\dfrac{5}{{3600}} = \dfrac{1}{{720}}\] hours
Now as we know that speed = \[\dfrac{{{\text{Distance travelled}}}}{{{\text{Time taken}}}}\]. So, the speed of the aeroplane will be equal to \[\dfrac{2}{{\dfrac{1}{{720}}}} = 2 \times 720 = 1400\]km/hr
So, the constant speed of the aeroplane will be 1440 km/hr.
Hence, the correct option will be D.

Note:- Whenever we come up with this type of problem then we have to first assume the horizontal distance between the elevation point on ground and the position of aeroplane initially and after 5 seconds as x and y. And after that we had to use the trigonometric formula for \[\tan \theta = \dfrac{{{\text{Height}}}}{{{\text{Base}}}}\] to form two equations for the given angles. Then on solving these equations we will get the value of x and y. And the distance travelled by the aeroplane is y – x. Now we have to change the unit of given time in seconds to hours and after that we can directly apply the speed formula to find the speed of the aeroplane. This will be the easiest and efficient way to find the solution of the problem.