Question

An aeroplane flies around a square, the side of which measures $ 100 $ miles each. The aeroplane covers at a speed of $ 100\;m.p.h. $ the first side, at $ 200\;m.p.h. $ the second side, at $ 300\;m.p.h. $ the third side and $ 400\;m.p.h. $ the fourth side. The average speed of the aeroplane around the square is:
(A) $ 190\; $
(B) $ 195\; $
(C) $ 192\; $
(D) $ 200\; $

Answer 1

Hint: To solve this question we have to consider the mathematical concept of the harmonic mean. The harmonic mean can be defined as the reciprocal of the average value of the reciprocal. Hence using this method we can find the value of the average speed of the aeroplane around the square.

Formula used:
 $ H = \dfrac{N}{{\sum {\dfrac{{{f_i}}}{{{x_i}}}} }} $
where $ H $ is the harmonic mean and $ N $ is the number of terms.

Complete Step-by-step solution
We will first consider that the plane is flying around the corner of the square and let it cover one side of the square of distance $ AB\; $ with a speed of $ 100\;m.p.h. $ and it then covers distance $ BC\; $ with the speed of $ 200\;m.p.h. $ after that it turns and covers the distance which is the third side of the side given by $ CD\; $ with the speed of $ 300\;m.p.h. $ going further it then covers a distance of $ AD\; $ which is the fourth side of the square with a speed of $ 400\;m.p.h. $ .

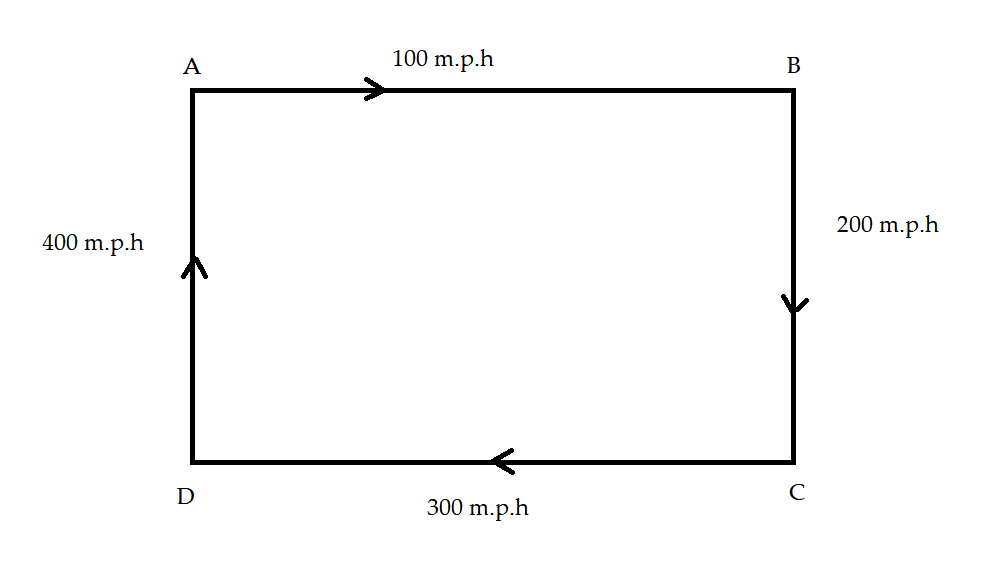
We have given that all side of square measures as
 $ AB = BC = CD = DA = 100 $ Miles.
Now to calculate the average speed of the plane around the square we have to use the harmonic mean method given by the formula,
 $ H = \dfrac{N}{{\sum {\dfrac{{{f_i}}}{{{x_i}}}} }} $
where $ H $ is the harmonic mean and $ N $ is the number of terms.
Hence the average velocity can be given in terms of harmonic mean such that
 $ {V_{avg}} = \dfrac{4}{{\dfrac{1}{{100}} + \dfrac{1}{{200}} + \dfrac{1}{{300}} + \dfrac{1}{{400}}}} $
 $ \Rightarrow {V_{avg}} = \dfrac{4}{{\dfrac{{12}}{{1200}} + \dfrac{6}{{1200}} + \dfrac{4}{{1200}} + \dfrac{3}{{1200}}}} $
Now we evaluate the total value to the denominator is given as
 $ {V_{avg}} = \dfrac{4}{{\dfrac{{12 + 6 + 4 + 3}}{{1200}}}} $
 $ \Rightarrow {V_{avg}} = \dfrac{4}{{\dfrac{{25}}{{1200}}}} $
Hence further simplification gives the value as
 $ {V_{avg}} = \dfrac{{4800}}{{25}} $
 $ \Rightarrow {V_{avg}} = 192m.p.h. $
Hence option (C) is the correct answer.

Note:
While dealing with such questions one should always ensure the proper method and proper units used in the questions. Here the units are given as $ \;m.p.h. $ which is miles per hours. We can also convert into the MKS system but it is required in the question to keep it as it is.