Question

An aeroplane can carry a maximum of 250 passengers. A profit of Rs.1500 is made on each executive class ticket and a profit of Rs.900 is made on each economy class ticket. The airline receives at least 30 seats for executive class. However at least 4 times as many passengers prefer to travel by economy class than by executive class. Formulate LPP in order to maximise the profit for the airline.

Answer 1

Hint: Here, we have to take the number of passengers in executive class as $x$ and the number of passengers in the economy class as $y$. With given data we will get the inequalities:
$x\ge 30$
$y\ge 4x$
$x+y\le 250$
For the equation $Z=1000x+600y$, we have to find the maximum Z by formulating LPP.

Complete step-by-step answer:
We are given that maximum number of passengers in an aeroplane = 250
 Profit made on each executive class = 1500
 Profit made on the economy class ticket = 900
Here, we have to formulate an LPP in order to maximise the profit.
Let us assume that the number of passengers on the executive class = $x$
The number of passengers on the economy class = $y$
We are also given that the seats given for executive class $\ge 30$
Therefore we can write:
$x\ge 30$ ….. (1)
We also have that at least 4 times as many passengers prefer to travel by economy class than by executive class.
By the given data we can write:
$y\ge 4x$
By taking $4x$ to the left side $4x$ becomes $-4x$. Hence, we obtain:
$y-4x\ge 0$ ….. (2)
Since, we are given that the maximum passengers in the plane is 250, we can write:
$x+y\le 250$ ….. (3)
We have the profit, $Z=1000x+600y$
Here, we have to maximise Z. Therefore, we have to consider:
$Maximise\text{ Z}=1000x+600y$
Now, combining all the constraints, we can write:
$\begin{align}
  & Maximise\text{ Z}=1000x+600y \\
 & x\ge 30 \\
 & y-4x\ge 0 \\
 & x+y\le 250 \\
 & x\ge 0 \\
 & y\ge 0 \\
\end{align}$
Now, we have to find the intersecting points of the lines of $x=30$ and $y-4x=0$.
For $x=30$, we have:
$\begin{align}
  & y-4\times 30=0 \\
 \Rightarrow & y-120=0 \\
 \Rightarrow & y=120 \\
\end{align}$
Therefore, the intersecting points are $(30,120)$
 Next, we have to find the intersecting points of $x=30$ and $x+y=250$.
For $x=30$, we have:
$30+y=250$
Now, by taking 30 to the right side it becomes -30, we get:
\[\begin{align}
  & y=250-30 \\
 \Rightarrow & y=220 \\
\end{align}\]
Therefore, the intersecting points are $(30,220)$.
Next, we have to find the intersecting points of $y-4x=0$ and $x+y=250$.
Consider, $y-4x=0$.
By taking \[-4x\] to the right side it becomes \[4x\], we get:
$y=4x$
 By substituting the value of y in equation $x+y=250$, we obtain:
$\begin{align}
  & x+4x=250 \\
 \Rightarrow & 5x=250 \\
\end{align}$
By cross multiplication we get:
$x=\dfrac{250}{5}$
By cancellation we get:
$x=50$
Now, $y=4x$ becomes:
$\begin{align}
  & y=4\times 50 \\
 \Rightarrow & y=200 \\
\end{align}$
Therefore, the intersecting points are $(50,200)$.
We, have the LPP given below:

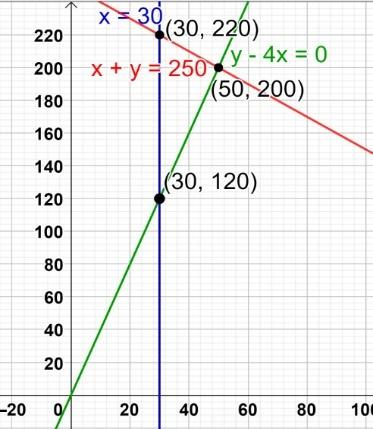
Now, we have to calculate Z for the corner points $(30,120)$, $(30,220)$, $(50,100)$.
For the point, $(30,120)$ we have:
$\begin{align}
  & Z=1000x+600y \\
\Rightarrow & Z=1000\times 30+600\times 120 \\
\Rightarrow & Z=30000+72000 \\
 \Rightarrow & Z=102000 \\
\end{align}$
For the point $(30,220)$we have:
$\begin{align}
  & Z=1000x+600y \\
 \Rightarrow & Z=1000\times 30+600\times 220 \\
 \Rightarrow & Z=30000+132000 \\
 \Rightarrow & Z=162000 \\
\end{align}$
For the point $(50,100)$ we have:
$\begin{align}
  & Z=1000x+600y \\
 \Rightarrow & Z=1000\times 50+600\times 100 \\
 \Rightarrow & Z=50000+60000 \\
 \Rightarrow & Z=110000 \\
\end{align}$
 From the above data we can say that the maximum value of Z is obtained at the point $(30,220)$.
Hence, the profit will be maximum, if
Tickets of executive class = 30
Tickets of economy class = 220
 Therefore, the maximum profit is Rs.162000.

Note: Here, you have to identify the common region of all the inequalities and you should get the corner points to evaluate maximum Z. So you should be careful while taking the corner points, if your points are wrong then the maximum Z will change.