Question

An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be ${45^ \circ }$ and ${60^ \circ }$ . Find the width of the river
A. $115.47\,m$
B. $200\,m$
C. $215.47\,m$
D. $315.47\,m$

Answer 1

Hint: To solve this question, we will draw the figure for easy calculation. and then we will apply the values of the trigonometric ratios to find the width of the river. Also, we should know that the angle of depression is the angle between the axis of the plane and the line joining the plane to the bank of the river.

Complete step by step answer:
So here, first we have to draw the figure for the given data. According to the given data we have an aeroplane flying at a height of $200m$ with angles of depression ${45^ \circ }$ and ${60^ \circ }$ with the river.

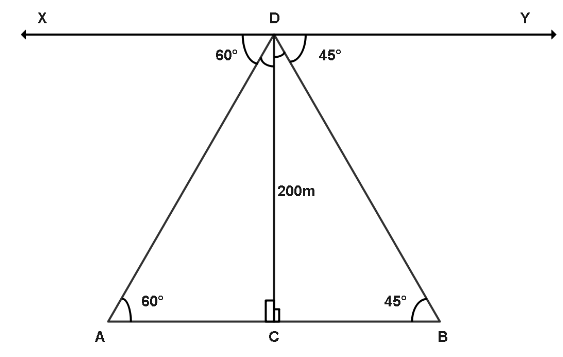
In the figure, let $D$ be the aeroplane at a height of $200m$ from the ground. i.e., $CD = 200m$ , let $AB$ be the width of the river. The angles of depression are:
$\angle ADX = {60^ \circ } \\
\Rightarrow \angle BDY = {45^ \circ }$
Here, let AD be the transversal drawn between the two parallel lines $XY$ and $AB$ . So, by the properties of transversal we say that the interior opposite angles are equal. i.e.
$\angle ADX = \angle BAD = {60^ \circ }$
Similarly, we can say that,
$\angle BDA = \angle ABD = {45^ \circ }$

To find the width of the river$AB$ , consider two triangles, $\vartriangle DAC$ and $\vartriangle DBC$. First, let us consider $\vartriangle DAC$ where tangent of $A$ is given by,
$\tan {60^ \circ } = \dfrac{{opposite{\text{ }}side}}{{Adjacent{\text{ }}side}} \\
\Rightarrow \tan {60^ \circ } = \dfrac{{CD}}{{AC}} \\ $
$ \Rightarrow \tan {60^ \circ } = \dfrac{{200}}{{AC}}$ -----(1)
Hence,
$\tan {60^ \circ } = \sqrt 3 \\
\Rightarrow AC = \dfrac{{200}}{{\sqrt 3 }} \\
\Rightarrow AC = 66.66\sqrt 3 \\ $
Now let’s consider $\vartriangle DBC$ where tangent of $B$ is given by,
$\tan {45^ \circ } = \dfrac{{opposite{\text{ }}side}}{{Adjacent{\text{ }}side}} \\
\Rightarrow \tan {45^ \circ } = \dfrac{{CD}}{{BC}} \\ $
$ \Rightarrow \tan {45^ \circ } = \dfrac{{200}}{{BC}}$ -----(2)
Hence,
$\tan {45^ \circ } = 1 \\
\Rightarrow BC = \dfrac{{200}}{1} \\
\Rightarrow BC = 200 \\ $
From the figure we can say that,
$AB = AC + BC \\
\Rightarrow AB = 66.66\sqrt 3 + 200 \\
\Rightarrow AB = 115.47 + 200 \\
\therefore AB = 315.47 \\ $
Hence, the correct option is D.

Note: To solve these types of problems, figure is necessary for the calculations. Here, $AD$ and $BD$ are transversals, a transversal is a line that cuts two or more lines, often parallel lines. From the figure we can say that $XY$ and $AB$ are parallel lines. Therefore, we can say that the alternate interior angles are equal.