Question

What is the ammeter reading of the given circuit?

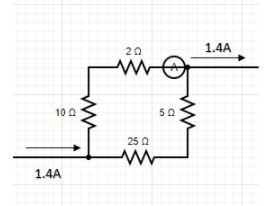
$\begin{align}
  & \text{A}\text{. 0}\text{.4A} \\
 & \text{B}\text{. }\text{1}\text{.0A} \\
 & \text{C}\text{. 0}\text{.6 A} \\
 & \text{D}\text{. 1}\text{.2A} \\
\end{align}$

Answer 1

Hint: Take the current in upper and lower loop to be ${{i}_{1}}$ and lower loop be ${{i}_{2}}$. Then apply Kirchhoff’s current law to the loop. Then the sum of the currents entering and leaving should be the same. From which you will get one equation containing ${{i}_{1}}$ and ${{i}_{2}}$. Then apply Kirchhoff’s voltage law to the whole loop and you will get another equation containing ${{i}_{1}}$and ${{i}_{2}}$. Solve these two equation to get the current in upper loop which will give the current through the ammeter.

Formula used:
$\begin{align}
  & \sum{I}=0 \\
 & \sum{\Delta V=0} \\
\end{align}$

Complete step-by-step answer:

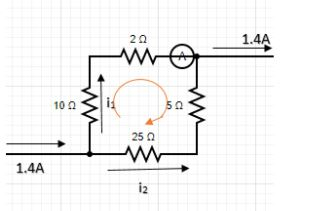
Consider the current through the upper arm be ${{i}_{1}}$ and the current through the lower arm be ${{i}_{2}}$.
Then according to Kirchhoff’s current law ${{i}_{1}}+{{i}_{2}}=1.4$
Applying Kirchhoff’s Voltage law we get
$\begin{align}
  & 10{{i}_{1}}+2{{i}_{1}}-5{{i}_{2}}-25{{i}_{2}}=0 \\
 & \Rightarrow 12{{i}_{1}}-30{{i}_{2}}=0 \\
 & \Rightarrow 2{{i}_{1}}-5{{i}_{2}}=0 \\
\end{align}$
So the two equations containing ${{i}_{1}}$ and ${{i}_{2}}$ is
${{i}_{1}}+{{i}_{2}}=1.4$and $2{{i}_{1}}-5{{i}_{2}}=0$
Solving these two equations.
${{i}_{2}}=1.4-{{i}_{1}}$ putting it other equation
\[\begin{align}
  & 2{{i}_{1}}-5{{i}_{2}}=0 \\
 & \Rightarrow 2{{i}_{1}}-5\left( 1.4-{{i}_{1}} \right)=0 \\
 & \Rightarrow 2{{i}_{1}}+5{{i}_{1}}-7=0 \\
 & \Rightarrow 7{{i}_{1}}=7 \\
 & \Rightarrow {{i}_{1}}=1A \\
\end{align}\]
So the correct option is $\text{B}\text{. }\text{1}\text{.0A}$

So, the correct answer is “Option B”.

Additional Information: Kirchhoff’s first law or Junction rule or Kirchhoff’s current rule: It states that in an electric circuit the algebraic sum of currents at any junction is zero. I.e. The sum of currents entering or leaving the junction is zero. Mathematically this law may be expressed as
$\sum{I}=0$
Sign convention for applying Junction rule:
(i)The current flowing towards the junction is taken as positive.
(ii)the currents flowing away from the junction is taken as negative.
Kirchhoff’s voltage law: This law states that around any closed loop of a network the algebraic sum of changes in potential must be zero. I.e.
\[\sum{\Delta V=0}\]
Sign convention:
(i) We can take any direction, clockwise or anti-clockwise as the direction of the loop.
(ii) the emf of the cell is taken as positive if the direction of the loop is from its negative to positive terminal of the battery.

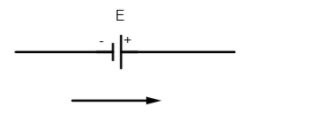
Here if the emf of cell is $E$ then the potential across the cell is $V=+E$ (positive emf)
(iii) the emf of the cell is taken as negative if the direction of the loop is from its positive to negative terminal of the battery.

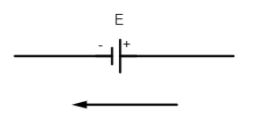
Here if the emf of cell is $E$ then the potential across the cell is $V=-E$ (negative emf)

(iv) The current-resistance $\left( IR \right)$ product is taken as positive if the resistance is travelled in the same direction as the assumed loop.

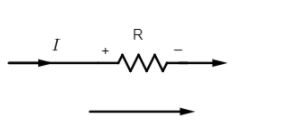
Here potential drop across the resistance R is $V=+IR$ (positive potential drop)
(v) The current-resistance $\left( IR \right)$ product is taken as negative if the resistance is travelled in the opposite direction as that of the assumed loop.

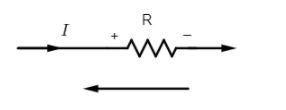
Here potential drop across the resistance R is $V=-IR$ (negative potential drop)

Note: Kirchhoff’s first law is based on the principle of conservation of charge when currents inside a circuit are steady, charges cannot accumulate or originate at any point on the circuit. So whatever charge flows towards a junction in any interval an equal charge must flow away from that junction in the same time interval.
Kirchhoff's second law or Kirchhoff’s voltage law is based on the principle of conservation of energy. This is because of the conservative nature of electrostatic force. As the electrostatic force is conservative the total work done by it along any closed path must be zero.