Question

Amit standing on a horizontal plane. Find a bird flying at a distance of 200 m from him at an elevation of $ 30{}^\circ $ . Deepak standing on the roof of a 50 m high building finds the angle of elevation of the same bird to be $ 45{}^\circ $ . Amit and Deepak are on opposite sides of the bird. Find the distance of the bird from Deepak.

Answer 1

Hint: Let the height of the bird from the ground be x meters. Then draw the diagram of the situation given in the question and apply the definition of sine trigonometric angle to get the value of x meters using the data that the distance between the bird and Amit is 200m. Then move to the case of Deepak and again use the sine trigonometric ratio to get the required answer.

Complete step-by-step answer:
Let us start the solution to the above question by letting the height of the bird from the ground be x meters.
Now, let us draw the situation of the above question by drawing the diagram of the situation given in the question.

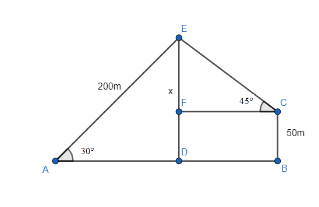
According to the above figure, Amit is at point A and Deepak is at point C. We have to find EC.
In $ \Delta ADE $ , we know that $ \angle EAD=30{}^\circ $ . Also, we know that $ \sin x=\dfrac{perpendicular}{hypotenuse} $ .
 $ \sin \left( \angle EAD \right)=\dfrac{ED}{EA}=\dfrac{x}{200} $
 $ \Rightarrow \sin 30{}^\circ =\dfrac{x}{200} $
Now, we know that $ \sin 30{}^\circ =\dfrac{1}{2} $ . If we put this in the above equation, we get
 $ \dfrac{1}{2}=\dfrac{x}{200} $
 $ \Rightarrow x=100 $
Now let us move to triangle EFC. We know that $ \angle ECF=45{}^\circ $ and EF=(x-50)=100-50=50m. So, if we again use the definition of sine function, we get
 $ \sin \left( \angle ECF \right)=\dfrac{EF}{EC} $
 $ \Rightarrow \sin 45{}^\circ =\dfrac{50}{EC} $
Now, we know that $ \sin 45{}^\circ =\dfrac{1}{\sqrt{2}} $ .
 $ \dfrac{1}{\sqrt{2}}=\dfrac{50}{EC} $
 $ EC=50\sqrt{2}m $
Therefore, the distance of the bird from Deepak is $ 50\sqrt{2}m $ .

Note: The key to the above question is getting the diagram correct. It is very often seen that students assume the distance in such questions to be the horizontal distance between the bird and the person, i.e., they consider the base to be the given distance but in actual it is the hypotenuse. Also, don’t convert $ 50\sqrt{2}m $ in decimal form until not asked or the value of $ \sqrt{2} $ is mentioned in the question. However, if you convert it is not wrong.