Question

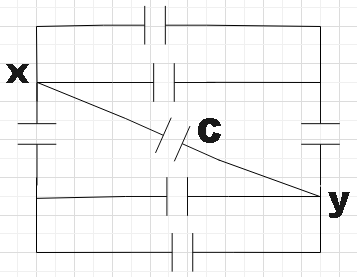
All the capacitors except C have capacitance of$2\mu F$. The capacitance of C, so that the total capacitance between x and y is $4\mu F$ will be

A. $\dfrac{4}{3}\mu F$
B. $\dfrac{3}{4}\mu F$
C. $\dfrac{2}{3}\mu F$
D. $\dfrac{3}{2}\mu F$

Answer 1

Hint: In the question, we have a very simple combination of few capacitors that are connected in series or parallel with each other. Just like how we find the effective capacitance across the mentioned terminal, we could cut-down the combination to a much simpler version of itself and thus find the answer.
Formula used:
Effective capacitance,
In series:
${{C}_{eff}}=\dfrac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}}$
In parallel,
${{C}_{eff}}={{C}_{1}}+{{C}_{2}}$

Complete answer:
In the question, we are given a combination of capacitors with one of them with capacitance C and all the others with capacitance$2\mu F$. We are supposed to find the capacitance C in the combination such that it satisfies the condition of net capacitance of the combination across XY terminals being$4\mu F$.
If you look at the combination carefully, you could clearly observe that the capacitors are connected symmetrically across the XY terminals. On either side we have two capacitors that are connected parallel and which is further connected in series with another.
We know that net capacitance of the parallel connection is given by the sum. That is,
${{C}_{eff}}={{C}_{1}}+{{C}_{2}}$
${{C}_{1}}=\left( 2+2 \right)\mu F=4\mu F$
The circuit could be now redrawn to get,

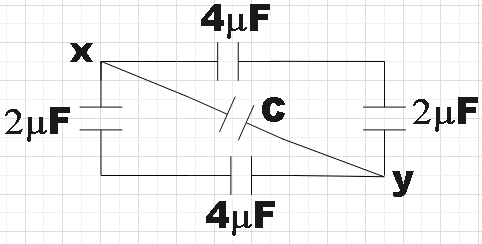
Now we have a $4\mu F$ capacitor connected to $2\mu F$ capacitor in series on either side of the capacitor of capacitance C. For series combination we have,
${{C}_{eff}}=\dfrac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}}$
${{C}_{2}}=\dfrac{4\times 2}{4+2}=\dfrac{8}{6}=\dfrac{4}{3}$
Circuit can now be again redrawn to get,

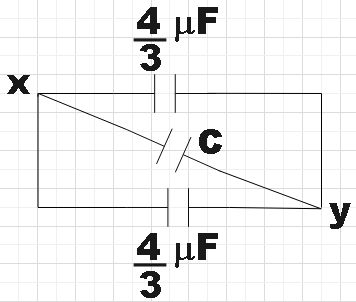
We have the effective capacitance across XY given to be $4\mu F$ and we have three capacitors connected in parallel across these terminals. So,
${{C}_{eff}}=\dfrac{4}{3}+C+\dfrac{4}{3}=4\mu F$
$\Rightarrow \dfrac{8}{3}+C=4$
$\therefore C=4-\dfrac{8}{3}=\dfrac{4}{3}$
Therefore, we found the unknown capacitance C to be$C=\dfrac{4}{3}\mu F$.

Hence, option A is the correct answer.

Note:
You may have noted very well that we have a symmetric connection across the capacitor of capacitance C. So, we found the effective capacitance for smaller combinations and did the reduction symmetrically across the mentioned terminals and hence found the answer accordingly.