Question

All surfaces are smooth in the adjoining figure. Mass of the wedge is \[M\] and the mass of the block is \[m\] . Find \[F\] such that the block remains stationary with respect to the wedge.

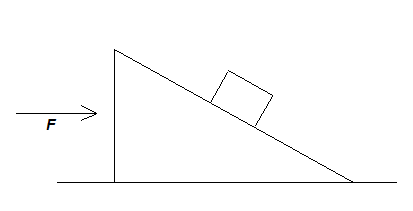
A. \[\left( {M - m} \right)g\tan \theta \]
B. \[\left( {M + m} \right)g\tan \theta \]
C. \[mg\tan \theta \]
D. \[Mg\tan \theta \]

Answer 1

Hint: First of all, we will calculate the acceleration of the system. Then we will equate the vertical and horizontal forces separately. Then we will manipulate the two equations and followed by substitution to obtain the desired result.

Complete step by step answer:
In the given problem, we are supplied with the following data:
Mass of the wedge is given as \[M\] .
Mass of the block is given as \[m\] .
We are asked to find the force such that the block remains stationary with respect to the wedge.

For this we need to draw the free body diagram of the arrangement to have a better understanding.

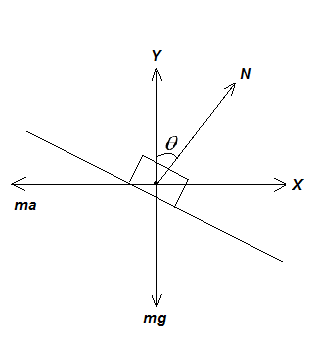
In the diagram, the weight of the body acts vertically in the downward direction. The normal reaction or the normal force acts in the upward direction perpendicular to the plane on which the block is resting. A pseudo force acts towards the left. The normal reaction is inclined at an angle \[\theta \] with the vertical.

To begin with, we will find the net acceleration of the arrangement containing both the block and the wedge i.e. we can say the combined system.
We know,
Force is given by the product of mass and acceleration.
\[F = \left( {M + m} \right)a\]
\[a = \dfrac{F}{{M + m}}\] …… (1)
The pseudo force with is acting along the horizontal direction towards left, cancels out the sine component of the normal reaction
Equating the vertical forces, we get:
\[\sum {{F_{\text{y}}} = 0} \]
\[N\cos \theta = mg\] …… (2)
Equating the horizontal forces, we get:
\[\sum {{F_{\text{x}}} = 0} \]
\[N\sin \theta = ma\] …… (3)
Now, we divide equation (3) by equation (2), and we get:
\[\dfrac{{N\sin \theta }}{{N\cos \theta }} = \dfrac{{ma}}{{mg}} \\
  \tan \theta =\dfrac{a}{g} \\
  a = g\tan \theta \\
\]
Now, substituting the values of the acceleration found, in the equation (1), we get:
\[
  g\tan \theta =\dfrac{F}{{M + m}} \\
  F = \left( {M + m} \right)g\tan \theta \\
\]
Hence, the force such that the block remains stationary with respect to the wedge \[\left( {M + m} \right)g\tan \theta \] .
The correct option is B.

Note:This problem can be solved easily if you have some basic knowledge on the free body diagrams. Many students seem to have confusion regarding the placement of the normal reaction. It is always present perpendicular to the plane of action, not just perpendicular to the ground always. It depends on the plane of action. While calculating the force, we must take both the bodies into account.