Question

“All rhombus are parallelograms”. Select the correct option regarding the above statement.
(a) True
(b) False

Answer 1

Hint: Check – out the different properties of parallelogram and compare it with the properties of rhombus to conclude about the given statement. Compare the properties of sides of both the quadrilaterals to get the answer.

Complete step by step answer:
We have been provided with the statement “All rhombuses are parallelogram” and we have to determine if it is true or false. First let us know about these quadrilaterals and their properties.
(i) Parallelogram: -
It is a quadrilateral in which opposite sides are equal and parallel.

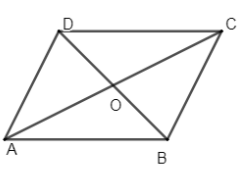
Here, in the above figure, AB = CD and BC = AD. Also, the sum of adjacent angles is equal to \[{{180}^{\circ }}\].
\[\Rightarrow \angle A+\angle B=\angle A+\angle D={{180}^{\circ }}\], same for \[\angle B,\angle C\] and \[\angle D\].
Opposite angles of the parallelogram are equal.
\[\Rightarrow \angle A=\angle C\] and \[\angle B=\angle D\].
Diagonals AC and BD bisect each other.
If we will make each angle of the parallelogram equal to \[{{90}^{\circ }}\] then it will become a rectangle.
(ii) Rhombus: -
It is a quadrilateral in which all sides are equal and opposite sides are parallel.

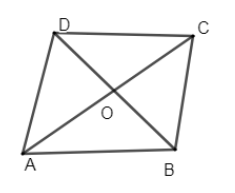
Here, in the above figure, AB = BC = CD = DA. Also, the sum of adjacent angles is equal to \[{{180}^{\circ }}\].
\[\Rightarrow \angle A+\angle B=\angle A+\angle D={{180}^{\circ }}\], same for \[\angle B,\angle C\] and \[\angle D\].
Opposite angles of the rhombus are equal.
\[\Rightarrow \angle A=\angle C\] and \[\angle B=\angle D\].
Diagonals AC and BD bisect each other at \[{{90}^{\circ }}\].
If we will make each angle of the rhombus equal to \[{{90}^{\circ }}\] then it will become a square.
On going through these various properties of both parallelogram and rhombus we conclude that rhombus has each and every property of parallelogram plus it has some additional properties. So, the conclusion can be, “all rhombuses are parallelograms”.

So, the correct answer is “Option A”.

Note: One may note that it is correct that “all rhombuses are parallelogram” but it’s reverse statement, “all parallelograms are rhombus” is not correct. This is because rhombuses have some additional properties which a parallelogram does not have. So, do not get confused in such statements and compare their properties for simplification.