Question

All circles are _____.
A. similar
B. congruent
C. Both similar and congruent
D. none of the above

Answer 1

Hint: Draw circles and compare their shape and size. And thus show that the circles can be similar or congruent.

Complete Step-by-Step solution:
Let us draw 2 circles to prove this question. From the figure, we can make out that both the circles have the same shape. But both the circles have the same shape. But both the circles are of different size. All circles have the same shape i.e. they are round. But the size of a circle may vary. Thus circles are similar.

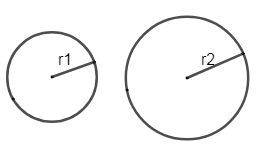
Each circle has a different radius so the size of the circle may vary.
Now if we are looking at both circles, let circle 1 have a radius \[{{r}_{1}}\] and circle 2 have a radius of \[{{r}_{2}}\]. From the figure we can make out that \[{{r}_{2}}\] is greater than \[{{r}_{1}}\]. i.e. radius of circle 2 is greater than radius of circle 1.
\[\therefore \] They are not of the same size, but of the same shape.
So we can say they are congruent.
We know that congruent means the same shape but different size. Different circles may have the same or different sizes.
\[\therefore \] All circles are both similar and congruent.
\[\therefore \] Option (c) is the correct answer.

Note: You know the general properties of a circle are, the outer line of a circle is equidistant from the center. The diameter of the circle divides it into two equal parts. And thus the circles which have equal radii are congruent to each other.